What is interest?
When you put money into a savings account, the bank will use your money, for example by lending it to other people.
They will pay you a certain amount for allowing this.
The money they pay you is known as ‘interest’.
The rate of interest is calculated on an annual basis or Each year. (% p.a.).
When you borrow money, you will have to pay interest as well as paying back the original amount.
The original amount of money borrowed or loaned is called the ‘principal’.
The ‘interest rate’ is the % of the principal that is added on over the course of one year as interest.
The interest rate charged or earned depends on a lot of factors, including the financial conditions in the country at the time.
The interest rate, including and fees charged over one year, to borrow money is known as Annual Percentage Rate, APR.
The interest rate, including and fees charged over one year, to lend money is known as Annual Equivalent Rate, AER.
APR and AER make it easier to compare savings accounts and loans.
A short video showing how to work out interest.
How much is £20 + 5% interest?
£20
100%
5%
105%
1.05
0.05
? = £20 x 1.05 = £21.00
How to work out interest
Image caption, Click to see a step-by-step slideshow.
1 of 7
Simple interest
Simple interest is calculated as a percentage of the principal and stays the same over time.
Example
Saoirse puts \(£250\) into a savings account which gives simple interest at a rate of \(7.5\%\) per annum (per year).
How much will Saoirse have saved after \(3\) years?
Every year, \(7.5\%\) of \(£250\) will be added as interest to Saoirse’s account.
\({7.5}\% {~of~} {£250} = {£18.75}\)
Each year \(£18.75\) interest will be added.
After \(3\) years interest to be added \(= {3}\times £18.75 = £56.25\).
Saoirse will have saved the principal + interest \(= £250 + £56.25 = £306.25\)
After \(3\) years Saoirse will have saved \(£306.25\).
Question
Rory borrows \(£300\) from his bank.
The bank charges \(9\%\) simple interest per annum.
How much will Rory owe after \(4\) years?
Answer
Each year, \(9\%\) of \(£300\) will be added to the amount that Rory owes.
\(9\%\) of \(£300 = £27\)
Each year \(£27\) interest will be added.
After \(4\) years \({4} \times £27 = £108\) will be added.
Rory will owe the principal + interest
\(= £300 + £108 = £408\)
After \(4\) years Rory will owe \(£408\).
Simple interest formula
It can be helpful to use a formula to calculate simple interest, provided you give the variables the correct values.
The formula is:
Simple Interest = \(\frac{(P ×T×R)}{100}\)
Where
P = Principal (in £s)
T = Time (in years)
R = Interest rate (\(\%\) p.a.)
Example
To show how the formula works, we can recalculate the last example:
Rory borrows \(£300\) from his bank.
The bank charges simple interest at a rate of \(9\%\) p.a. (per annum).
How much will Rory owe after \(4\) years?
P = \(£300\)
T = \(4\) years
R = \(9\%\) p.a.
Put these values into the formula.
Simple Interest = \(\frac{(300 × 4 × 9)}{100}\)
\(= £108\)
Rory owes \(£108\) interest + the principal of \(£300\)
\(= £408\)
If you are using the formula to calculate simple interest, don’t forget to add the principal if you want to know the total amount owed/saved.
Question
Use the simple interest formula to calculate the interest gained on \(£2500\) over \(4\) years at a rate of \(6\%\) per annum.
Answer
Simple Interest = \(\frac{(P × T × R)}{100}\)
P = \(£2500\)
T = \(4\) years
R = \(6\%\) p.a.
Interest = \(\frac{({2500}\times{4}\times{6})}{100}\)
\(= £600\)
Compound Interest
Compound interest is interest that is calculated on the principal plus the amount of interest already earned.
Therefore, the amount of money that earns interest increases every year.
Example
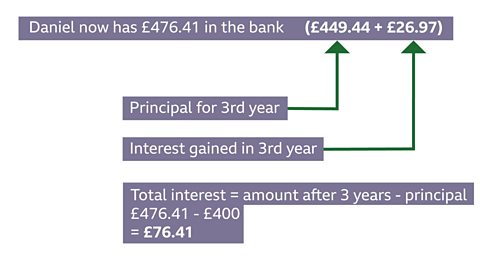
Daniel invests \(£400\) at a compound interest rate of \(6\%\).
How much interest will he have earned after \(3\) years?
Interest earned in first year
\(= 6\% ~of~ £400\)
\(= £24\)
Principal for second year
\(= £400 + £24\)
\(= £424\)
Interest earned in second year
\(= 6\%~ of~ £424\)
\(= £25.44\)
Principal for second year
\(= £424 + £25.44 = £449.44\)
Interest earned in third year
\(= 6\%~ of ~£449.44\)
\(= £26.97\)
Total amount of interest earned
\(= £24 + £25.44 + £26.97\)\(= \boldsymbol{£76.41}\)
Question
Amelia borrows \(£1500\) at a compound interest rate of \(8\%\) per annum (p.a.).
How much does she owe after \(2\) years?
Answer
Interest to be added in first year
\(= 8 \percent~of~£1500\)
\(= £120\)
Principal for second year
\(= £1500 + £120\)
\(= £1620\)
Interest to be added in second year
\(= 8 \percent~of~£1620\)
\(= £129.60\)
Amelia now owes \(= £1620 + £129.60\)
\(= \boldsymbol{£1749.60}\)
Compound Interest Formula
If compound interest is to be added over a large number of years, the calculation becomes very long and complex. In this case, it is convenient to use a formula.
Total amount \(= {P}\times{(1 +}\frac{R}{100})^t\)
P = Principal (original amount)
R = compound interest rate (%)
T = time (years)
Example
Daniel invests \(£400\) at a compound interest rate of \(6\%\).
How much interest will he have earned after \(8\) years?
P = \(£400\)
R = \(6\%\) per annum (p.a.).T = \(8\) years
Total amount after \(3\) years \(= {P}\times{(1 +}\frac{R}{100})^t\)\(= 400 (1 + 0.06)^8\)
\(= 400(1.06)^8\)
\(= £637.54\)
Interest earned \(= £637.54 - £400 = £237.54\)
Question
Ryan borrows \(£850\) at a compound interest rate of \(9 \percent\) per annum (p.a.).
Use the compound interest formula to calculate how much will he owe after \(4\) years?
Answer
P = \(£850\)
R = \(9 \percent\) per annum (p.a.).
T = \(4\) years
Total amount after \(4\) years \(= {P}\times{(1 +}\frac{R}{100})^t\)
\(= 850\times(1 + 0.09)^4\)
\(= 850\times(1.09)^4\)
\(= £1199.84\) (nearest penny)
Ryan owes \(£1199.84\) after \(4\) years.
Test section
Question 1
Calculate the simple interest on \(£7000\) borrowed for \(5\) years at an interest rate of \(5.5\%\) per annum (p.a.).
Answer
\(£1925\)
Question 2
Jamie puts \(£450\) into a savings account.
How much will he have in his account after \(4\) years at a simple interest rate of \(12\%\) per annum (p.a.)?
Answer
\(£666\)
Question 3
Emily invests \(£1200\).
After four years, how much will her investment be worth if she is paid \(12\%\) compound interest per annum?
Answer
\(£1888.22\)
Question 4
Mo borrows \(£2400\) at 1\(5\%\) per annum (p.a.) compound interest for \(4\) years.
How much compound interest will he have to pay ?
Answer
\(£1797.62\)
More on Percentages
Find out more by working through a topic
- count4 of 9
