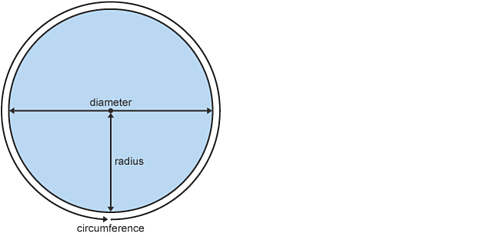
Investigating polygons
A polygon is a two dimensional shape enclosed by three or more straight lines.
A short video showing how to prove the sum of the angles in a n-sided polygon is 180° × (n-2). For example a hexagon has 6 sides, so (n-2) is 4, and the internal angles add up to 180° × 4 = 720°.
How to show angles in a n-sided polygon add to 180° × (n-2)

Image caption, Click to see a step-by-step slideshow.

Image caption, WHAT YOU NEED: ruler, scissors, pencil, card/paper, coloured pens.

Image caption, STEP 1: Use a ruler and pencil to draw an irregular hexagon. A hexagon has six sides so n=6. Use the scissors to cut the shape out.
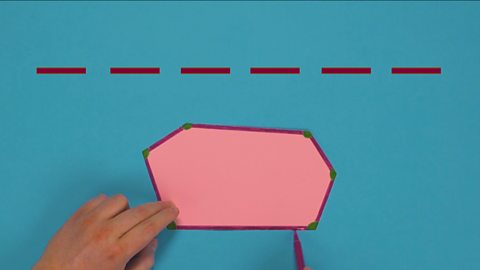
Image caption, STEP 2: Use a pen to draw on and colour in the angles. Then use a different pen and a ruler to draw a coloured line along each side.
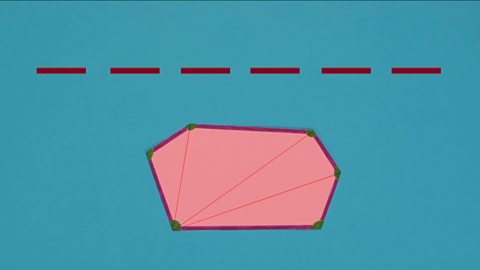
Image caption, STEP 3: Use a ruler to draw lines from the bottom left corner to the three opposite angles. We can ignore the two angles that are directly next to the starting point, because they already have lines along the sides linking them.

Image caption, STEP 4: Use the scissors to cut along the lines. You should be left with four triangles. Notice that the number of triangles is two less than the number of sides of the original polygon. The angles in each triangle add up to 180°.

Image caption, All the angles coloured in the original polygon are now in the triangles. To find the total we just multiply the number of triangles by 180°. So the sum of the angles in the original hexagon is 180° x (n-2) = 180° x 4 = 720°. You've done it!
1 of 7
The exterior angle of a polygon
The exterior angle at a vertex (corner) of a shape is made by extending a side.
Sum of exterior angles
The exterior angles of a polygon add up to \(360^\circ\).
Imagine walking round the outside of the polygon.
By the time you get back to where you started you have completed one full turn.
So all the corners you turned must add to \(360^\circ\).
In this diagram the exterior angles have been given different colours.
You can see how they can be put together to make a full circle.
The interior angle of a polygon
An interior angle is the angle inside the polygon at a vertex. The interior and exterior angles together lie on a straight line.
For each vertex of a polygon: \(interior~angle + exterior~angle = 180 ^\circ\)
Angles of a regular polygon
You have already seen that the sum of the exterior angles is \(360^\circ\) and that the interior and the exterior angles add up to \(180^\circ\).
A regular polygon is a polygon whose interior angles are all equal.
Use this information to find the exterior and interior angles of a regular polygon.
Question
Find the exterior and interior angle of a regular pentagon.
Answer
A pentagon has \({5}\) sides and \({5}\) exterior angles.
The exterior angles add up to \(360^\circ\).
\(one~exterior~angle = 360^\circ \div 5 = 72^\circ\)
\(interior~angle = 180 - exterior~angle = 180 - 72 = 108^\circ\)
Test section
Question 1
What is a polygon?
Answer
A polygon is a 2D shape with straight sides.
Question 2
What type of polygon is this shape?
Answer
A shape with five sides is called a pentagon.
Question 3
What is the sum of the interior angles in a pentagon?
Answer
The sum of the interior angles in a pentagon is \({540}^\circ~({180}^\circ\times{3})\).
Question 4
What is the sum of the interior angles in a decagon?
Answer
The sum of the interior angles in a decagon is \({1440}^\circ~({180}^\circ\times{8})\).
Question 5
What is the sum of the exterior angles of a quadrilateral?
Answer
The exterior angles of any polygon add up to \({360}^\circ\).
Question 6
What is the sum of the exterior angles of an octagon?
Answer
The exterior angles of any polygon add up to \({360}^\circ\).
Question 7
Five of the six exterior angles of an irregular hexagon measure \({15}^\circ\), \({30}^\circ\), \({45}^\circ\), \({110}^\circ\) and \({120}^\circ\).
What is the size of the sixth exterior angle?
Answer
The exterior angles of any polygon add up to \({360}^\circ\), so \({360}^\circ-{120}^\circ-{110}^\circ-{45}^\circ-{30}^\circ-{15}^\circ={40}^\circ\).
Question 8
Four of the five interior angles of an irregular pentagon measure \({155}^\circ\), \({60}^\circ\), \({75}^\circ\) and \({100}^\circ\).
What is the size of the fifth interior angle?
Answer
The interior angles of a pentagon add up to \({540}^\circ~({180}^\circ\times{3})\), so \({540}^\circ-{155}^\circ-{60}^\circ-{75}^\circ-{100}={150}^\circ\).
Question 9
What is the size of an interior angle of a regular pentagon?
Answer
The interior angles of a pentagon add up to \({540}^\circ~({180}^\circ\times{3})\).
So in a regular pentagon, an interior angle is \({540}^\circ\div{5}={108}^\circ\).
Question 10
What is the size of an interior angle of a regular hexagon?
Answer
The interior angles of a hexagon add up to \({720}^\circ~({180}^\circ\times{4})\).
So in a regular hexagon, an interior angle is \({720}^\circ\div{6}={120}^\circ\).
More on 2D shapes
Find out more by working through a topic
- count3 of 6

- count6 of 6