What is pi?
For any circle, \(circumference \div diameter = 3.141592…\)
This number is so special that it is given its own symbol \(\pi\) (the Greek letter pi).
The value \(\pi\) is a constant, but is called an irrational number as an exact value for \(\pi\) does not exist.
In non-calculator working out, approximate values of \(\pi\) are used, of which \(3.14\) and \(3.142\) are probably the most common.
Other, less accurate approximations of \(\pi\) are \(\frac{22}{7}\) and \(3\).
All scientific calculators have a \(\pi\) button.
You can use this to make your calculations more accurate.
A short video demonstrating pi.
History
The earliest known use of the Greek letter \(\pi\), to represent the ratio of a circle's circumference to its diameter, was by the Welsh mathematician William Jones in his 1706 work ‘Synopsis Palmariorum Matheseos’ or ‘A New Introduction to the Mathematics’.
Circumference
We know that \(circumference \div diameter = \pi\)
It therefore follows that \(circumference = \pi \times diameter\).
This can also be written as:
\(C = \pi d\)
The diameter is twice the length of the radius.
So, an alternative formula for the circumference of a circle is:
\(C = 2 \pi r\)
A one-minute video on how to show the circumference of a circle is π x diameter. π is 3.14 to 2 decimal places.
Circumference of circle slideshow

Image caption, WHAT YOU NEED: 3 glasses, ribbon, scissors.

Image caption, STEP 1 - WRAP RIBBON: Take the ribbon and wrap it around a glass. Mark where the ribbon overlaps itself.

Image caption, STEP 2 - CUT CIRCUMFERENCE: Cut the ribbon at the point where it overlaps. You now have a piece of ribbon which is the same length as the circumference of the glass.

Image caption, STEP 3 - LINE UP 3: Line up the other 2 glasses alongside the first so you have a row of 3 circles. The total length across is now 3 diameters.

Image caption, STEP 4 - π × DIAMETER: Place the ribbon across the top of the 3 glasses…

Image caption, …and you can see that the ribbon is just over 3 times the diameter of 1 circle. This number, called π (or pi), is approximately 3.14. You have shown that the circumference of a circle is π × diameter.

Image caption, TIP: Try it with any circular object. Whatever the size, the circumference is always just over 3 × diameter.
1 of 7
Question
A circle has a diameter of \({10~cm}\). Work out its circumference, using \(\pi = 3.14\).
Answer
Using \(C = \pi d\)
\(C = 3.14 \times 10\)
\(C = 31.4~cm\)
Using \(C = 2 \pi r\)
\(C = 2 \times 3.14 \times 5\)
\(C = 31.4~cm\)
Question
Anish and Becky each have a circular pond in their garden.
Anish's pond has a diameter of \({6~m}\).
Becky's pond has a diameter of \({3~m}\).
Anish says that the circumference of his pond is twice the circumference of Becky's pond.
a) Find the circumference of each pond, using \(\pi = 3.14\).
b) Is Anish's statement correct?
Answer
a) The circumference of Anish's pond is \({18.84~m}\) and the circumference of Becky's pond is \({9.42~m}\).
b) From the answers to a) you can see that Anish's statement is correct.
Area of a circle
The formula for working out the area of a circle is:
\(A = \pi r^2\), where \(r\) is the radius of the circle.
\(\pi r^2\) means \(\pi \times r \times r\).
Only the \(r\) is squared.
A one-minute video showing how to prove the area of a circle is π x r².
How to show the area of a circle is π x r2

Image caption, WHAT YOU NEED: Paper, compass, scissors, ruler, pencil and pen.

Image caption, STEP 1 - CUT OUT CIRCLE: Use the compass to draw a circle on the paper. Cut it out, fold it in half and use the ruler to draw a line along the fold.

Image caption, STEP 2 - CUT INTO SEGMENTS: Fold it in half again and use a ruler to draw a line along the fold. Repeat twice more until you have 8 equal sectors marked in the circle...

Image caption, ...then colour in half of the sectors before cutting them all out. You should now have 8 sectors.

Image caption, STEP 3 - MAKE A PARALLELOGRAM: Rearrange the sectors with four on the bottom and four on top, to form a shape that looks a bit like a parallelogram.

Image caption, STEP 4 - RECTANGLE IS πr x r : Fold the end sector in half and cut along the fold to make two half sectors. Put one at each end to form a shape close to a rectangle...

Image caption, ...the rectangle's height is just the radius of the circle, or 'r' for short. Its base is almost exactly the curved outsides of the coloured sectors, or half the circumference of the circle. So if the circumference is 2πr., the base must be πr.
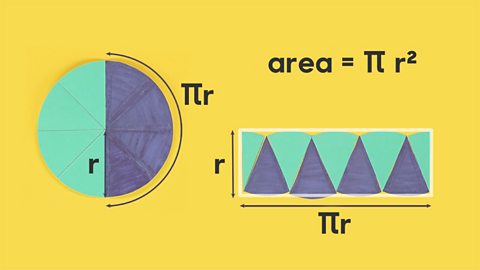
Image caption, The area of a rectangle is base x height. So if the base is πr and the height is r, the area of the rectangle is πr x r. Another way of writing this is π r², because r x r = r². TIP: π is just over 3, so the area of a circle is roughly 3 x r².
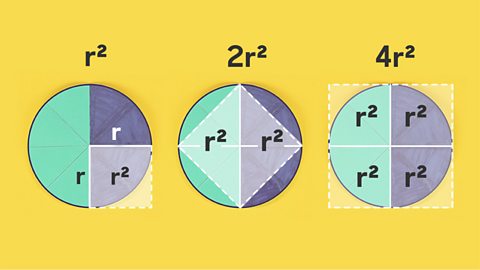
Image caption, TIP: A quick way to remember the area of a circle is to imagine an r x r square. Its area is r x r = r². Now if you imagine slicing this square diagonally you can see that the area of the circle is more than 2 r². But less than 4 r². So roughly 3 r².
1 of 9
Question
Find the area of the following circles, using \(\pi = 3.14\).
a) a circle of radius \({6~cm}\)
b) a circle of diameter \({10~cm}\)
Answer
a) \(r = 6~cm\), so we calculate:
\(A = 3.14 \times 6 \times 6 = 113.04~cm^2\)
b) The diameter is \({10~cm}\), so the radius is \({5~cm}\).
We calculate: \(A = 3.14 \times 5 \times 5 = 78.5~cm^2\)
Question
The dartboard above has a radius of \({20~cm}\).
The bullseye in the centre of the board has a radius of \({1~cm}\).
By calculating the area of the two circles, work out the area of the dartboard outside of the bullseye, using \(\pi = 3.14\).
Answer
Remember, the area of the large circle is \({3.14}\times{20}\times{20} = {1,256}~cm^{2}\).
The area of the small circle is \(3.14 \times 1 \times 1 = 3.14~cm^2\).
So, the area of the dartboard outside of the bullseye is \({1,256} - {3.14} = {1,252.86}~cm^{2}\).
Key point
When calculating the area of a circle, remember to use the radius, not the diameter.
How many times do the wheels on a scooter go round during a lap of the park?
How to work out circumference, diameter and the area of a circle.
Sophie Can we stop for a break now Ati?
Ati But Sophie, we’ve only just got to the cycle path.
Sophie But my poor roller-skates have only got little wheels.
Ati Hey, I wonder whose wheels really will work harder, your roller-skates' or my scooter’s?
Sophie Yeah. Ummm…
Mathsmutt! We need your help.
Mathsmutt Well guys, it all depends on the size of your wheels.
Ok, now give ‘em a push.
Sophie The bigger wheel takes longer to turn round.
Ati But how can we work out how many times our wheels go round during a lap of the park?
Mathsmutt Well, we know the path is 1000 metres long, so all we need to know now is how big the wheels are.
Let’s break it down!
The diameter of Sophie’s wheel is 0.06 metres.
Circumference is equal to π x diameter right? And, because we know diameter is two times the radius, we can use the equation C =2 x π x r…
Or C = π × D!
Sophie OK so if circumference is π x 0.06 that makes… 0.1885 metres.
Mathsmutt And Ati’s wheels have a diameter of 0.08 metres. So their circumference must be…?
Sophie 0.2513 metres! Now all we need to do is work out how many of these there are in the whole of the 1000 metre long path.
Mathsmutt Correctamundo! Now get your skates on!
Sophie So Ati, for my small wheels we divide 1000m by 0.1885m. That's 5305 revolutions.
Ati And for mine, we divide 1000 by 0.2513.
Sophie That means your big wheels only do 3979 revolutions.
Hey wait for me!
Mathsmutt What?
Ati Wow, I never knew this park was so big.
Mathsmutt Well, seeing as we're ‘on a roll’ Ati, I can tell you exactly how big it is. To find the area of a circle you just do π x Radius squared.
Here hold this Sophie.
Ok the radius is 159.15 metres. So we do π x 159.15 squared.
Ati That’s 79572.5 square metres.
Sophie Yay! Oops! Good boy.
Mathsmutt(mumbles) Sorry. So does all that make sense, or are your heads still spinning?
Sophie Well, it ‘turns’ out that circles are ‘wheelie’ easy, when you know how.
All Hehehe!
Test section
Question 1
What is a commonly used value of \(\pi\)?
a) \({3.14}\)
b) \({3.16}\)
c) \({13.5}\)
Answer
\({3.14}\) is the commonly used value of \(\pi\).
So, the correct answer is a).
Question 2
Which of the following is not a formula to find the circumference of a circle?
a) \(\pi{r}^{2}\)
b) \(\pi{d}\)
c) \({2}\pi{r}\)
Answer
The correct answer is a) \(\pi{r}^{2}\).
Question 3
What is the formula to find the area of a circle?
a) \(\pi{d}\)
b) \(\pi{r}^{2}\)
c) \({2}\pi{r}\)
Answer
The correct answer is b) \(\pi{r}^{2}\).
Question 4
What is the circumference of a circle that has a diameter of \({7}~{cm}\)?
Answer
The formula for circumference is: \({circumference}=\pi\times{d}\). so \(\pi\times{7}~{cm}={22.0}~{cm}~(to~1~dp)\).
Question 5
What is the circumference of a circle that has a radius of \({5}~{cm}\)?
Answer
The formula for circumference is: \({C}={2}\times\pi\times{r}\) or \({C}=\pi\times{d}\). \(\pi\times{5}\times{2}={31.4}~{cm}~(to~1~dp)\).
Question 6
What is the diameter of a circle that has a circumference of \({15}~{cm}\)?
Answer
The formula for diameter is \({d}=\frac{C}{\pi}\).
In this case, \({d}=\frac{15}{\pi}={4.8}~{cm}~(to~1~dp)\).
Question 7
What is the area of a circle that has a radius of \({5}~{cm}\)?
Answer
\(\pi\times{r}^{2}\) is the formula for the area of a circle.
\(\pi\times{5}^{2}=\pi\times{25}={78.5}~{cm}^{2}~(to~1~dp)\).
Question 8
What is the area of a circle that has a diameter of \({16}~{cm}\)?
Answer
\({A}=\pi\times{r}^{2}\) is the formula for the area of a circle.
\({d}={16}~{cm}\), so \({r}={8}~{cm}\).
\({A}=\pi\times{8}^{2}=\pi\times{64}={201.1}~{cm}^{2}~(to ~1~dp)\).
Question 9
What is the area of a half circle that has a radius of \({10}~{cm}\)?
Answer
\(\pi\times{r}^{2}\) is the formula for the area of a circle.
Therefore, the area of a half circle \(=\frac{(\pi\times{r}^{2})}{2}\).
\(\frac{(\pi\times{10}^{2})}{2}={157.1}~{cm}^{2}~(to~1~dp)\).
Question 10
What is the radius of a circle that has an area of \({42}~{cm}^{2}\)?
Answer
\({A}=\pi\times{r}^{2}\) is the formula for the area of a circle.
The formula to find the radius is \({r}=\sqrt\frac{A}{\pi}\).
Therefore, \({r}=\sqrt\frac{42}{\pi}\) which is \({3.7}~{cm}~(to~1~dp)\).
More on 2D shapes
Find out more by working through a topic
- count1 of 6
- count2 of 6
- count3 of 6
