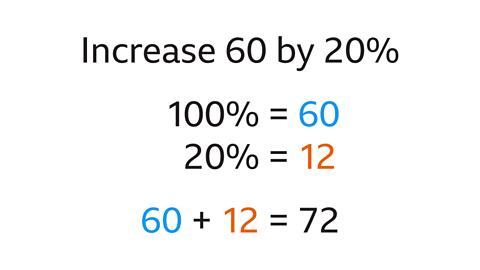How to work out interest

Key points

When money is borrowed, is charged. The amount of interest to be paid is calculated using the (which is a ), usually over a year ().
Investing money generates interest too. As the investment generates interest, its value increases.
is calculated on a fixed amount, so the amount of interest is the same.
is calculated on a changing amount. As interest is added the amount grows and so the interest also increases.
To calculate the interest, you need to be able to work out percentages of an amount and convert between percentages and decimals.
When calculating interest you may need to round numbers, for example to the nearest penny.

How to calculate the new amount given the interest rate

To calculate the new amount given the interest rate:

Work out the percentage of the amount. This is the interest. The interest rate gives the percentage.
Add the interest to the original amount.

There are different ways to find the percentage of an amount. Choose your preferred method:

Combine other percentages. For example, 20% is two lots of 10%
Use . For example, 20% is the same as \( \frac{1}{5} \)
Use a calculator. For example, to work out 20%, divide 20 by 100 and multiply by the amount.

Examples

Skip image gallery

Image caption,
£2000 is invested at a rate of 1∙5% interest per year. Find the amount of interest earned and the value of the investment after one year.
Image caption,
The initial investment is £2000, which is 100%. The interest rate is 1∙5%, which is the percentage to be added on.
Image caption,
Work out the percentage (1∙5%) of the amount (2000). The percentage of the amount is 30, so the interest is £30
Image caption,
Add the interest (30) onto the original amount (2000). The value of the investment after one year is £2030
Image caption,
£3000 is borrowed. The interest charged is 8%. Find the total to be repaid.
Image caption,
The original borrowed amount is £3000, which is 100%. The interest rate is 8%, which is the percentage to be added on.
Image caption,
Work out the percentage (8%) of the amount (3000). The percentage of the amount is 240, so the interest is £240.
Image caption,
Add the interest (240) onto the original amount (3000). The total amount to be repaid is £3240

Question

£7000 is borrowed to buy a car at a rate of interest of 15%.

What is the total amount to be repaid?

How to calculate compound interest

As interest is added the amount grows and so the interest also increases. An amount may be invested for more than one year.

To work out the total by the end of the investment period, calculate the interest for the first year and add it to the total. Then calculate the new interest for the second year and add that to the total. Repeat this for each year of investment. is calculated on a changing amount.

To simplify the calculation, a can be used to calculate the new total amount of an investment.

Use the interest rate to work out the multiplier.
Multiply the original value of the investment by the multiplier for each year the amount is invested.

For help on working out percentages using multipliers, it may be helpful to look at increasing an amount by a percentage.

Examples

Skip image gallery

Image caption,
£200 is invested at a rate of 5% per annum for two years. Find the value of the investment at the end of two years.
Image caption,
£200 is invested at a rate of 5% per annum for two years. After one year the investment is £200 + £10 = £210
Image caption,
In the second year the interest is 5% of £210 which is £10∙50. After two years the investment is £210 + £10∙50 = £220.50
Image caption,
The calculation can be simplified using a multiplier. The multiplier for an increase of 5% is 1∙05
Image caption,
The interest is applied twice. The investment (200) is multiplied by the multiplier (1∙05) twice.
Image caption,
The resulting value of investing £200 at an interest rate of 5% for two years is 200 × 1∙05 × 1∙05. This calculation can be written as 200 × 1∙052. After two years the investment is worth £220.50
Image caption,
£500 is invested for three years at an interest rate of 4%. Find the resulting value of the investment after three years.
Image caption,
Work out the multiplier. The multiplier for an increase of 4% is 1∙04
Image caption,
The resulting value of investing £500 at an interest rate of 4% for three years is 500 × 1∙04 × 1∙04 × 1∙04. This calculation can be written as 500 × 1∙04³. After rounding to the nearest penny, the investment is worth £562.43 after three years.

Question

£400 is invested at an interest rate of 3% for two years.

Find the total amount after two years.

How to work out a percentage change

The percentage change between two amounts is calculated by:

working out the difference between the two amounts
dividing by the original amount
multiplying the result by 100

The change could be an increase or a decrease.

Examples

Skip image gallery

Image caption,
£200 is invested for two years at an interest rate of 5%. The resulting value of the investment is £220.50. Find the percentage increase.
Image caption,
The difference between the two amounts is £20.50
Image caption,
The percentage change between 200 and 220.50 is calculated by working out the difference between 200 and 220.50, dividing by the original amount of 200 and multiplying the result by 100. The percentage change is an increase of 10.25% 10.25%
Image caption,
£500 is invested for three years at an interest rate of 4%. The resulting value of the investment is £562.43. Find the percentage increase.
Image caption,
The difference between the two amounts is £62.43
Image caption,
The percentage change between 500 and 562.43 is calculated by working out the difference between 500 and 562.43, dividing by the original amount of 500 and multiplying the result by 100. The percentage change is an increase of 12.486%
Image caption,
£1500 is invested in a scheme. The value at the end of the first year is £1200. Find the percentage decrease.
Image caption,
The percentage change between 1500 and 1200 is calculated by working out the difference between 1500 and 1200, dividing by the original amount of 1500 and multiplying the result by 100. The percentage change is a decrease of 20%

Practise working out interest

Try this quiz to practise what you've learned about working out interest.

Quiz

Real-world maths

A man using a calculator. — Image caption,
Using a calculator to calculate interest.

Anyone saving money will compare interest rates to get the best deal for themselves. Sometimes higher rates of interest are offered on savings accounts where you cannot withdraw money for a fixed period.

A shop may offer a deferred payment, so instead of paying £1500 in one go, you can pay over a longer period with interest added. Being able to calculate the total money owed including interest is important to make sure repayments are manageable and can be made in time.