KS3

How to find the original value before percentage off

Part ofMathsPercentages

Key points

involves working backwards through a calculation to find the original amount (before a ).
Understanding for increasing and decreasing by a percentage and being able to convert between decimals and percentages are important skills when calculating the original amounts.

Using 1% to find the original amount before percentage change

To find the original value of an amount before the percentage increase/decrease:

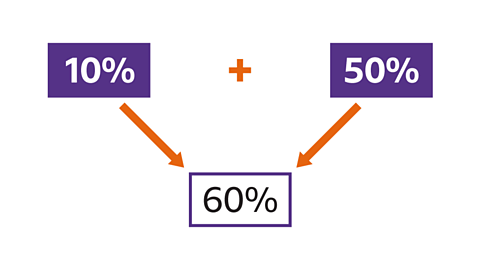
Write the amount as a percentage of the original value.
Find 1% of the original value.
The original value is 100%, so multiply by 100 to give the original value.

Examples

Skip image gallery

Image caption,
A price is increased by 30% to give £52. Find the original price.
Image caption,
The original price (100%) is increased by 30% giving a total of 130%. £52 is 130% of the original price.
Image caption,
Find 1% of the original price by dividing by 130. 52 ÷ 130 = 0∙4. 1% of the original price is £0∙40 (40p).
Image caption,
Find the original price by multiplying £0.4 by 100. The original price is £40. £40 increased by 30% is 52
Image caption,
A coat is reduced by 20% to £120. Find the original price.
Image caption,
The original amount (100%) is decreased by 20% which leaves 80%. £120 is 80% of the original price.
Image caption,
Find 1% of the original price by dividing 120 by 80. 1% of the original price is £1∙50
Image caption,
Work out the original price (100%) by multiplying 1% (£1∙50) by 100. 1∙5 ×100 = 150 The original price is £150

Question

A game is reduced by 15% in a sale. The sale price is £17. What was the original price?

Using a multiplier to find the original amount

To find the original amount of an amount before the percentage increase/decrease:

Find the for the .
Divide the amount by the multiplier.

Examples

Skip image gallery

Image caption,
A value is increased by 30% to give 52. Find the original amount.
Image caption,
Find the multiplier. The original amount (100%) is increased by 30% giving a total of 130%. The amount (52) is 130% of the original amount. 130 divided by 100 gives the multiplier. The multiplier is 1∙3
Image caption,
The original amount multiplied by the multiplier (1∙3) gives the amount (52). The amount (52) divided by the multiplier (1∙3) gives the original amount.
Image caption,
Find the original amount by dividing the amount (52) by the multiplier (1∙3). The original amount is 40. 40 increased by 30% is 52
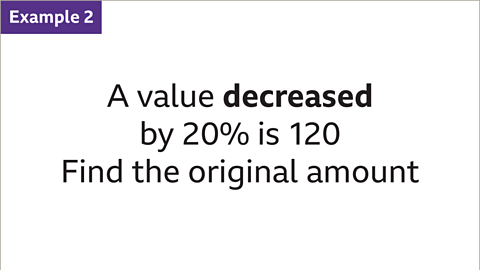
Image caption,
A value is decreased by 20% to give 120. Find the original amount.
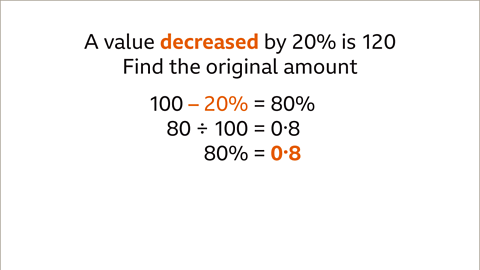
Image caption,
Find the multiplier. The original amount (100%) is decreased by 20% which leaves 80%. The amount (120) is 80% of the original amount. 80 divided by 100 gives the multiplier. The multiplier is 0∙8
Image caption,
The original amount multiplied by the multiplier (0∙8) gives the amount (120). The amount (120) divided by the multiplier (0∙8) gives the original amount.
Image caption,
Find the original amount by dividing the amount (120) by the multiplier (0∙8). The original amount is 150. 150 decreased by 20% is 120

Practise how to find the original value before percentage off

Practise finding the original value before percentage off with this quiz.

Quiz

Real-world maths

A white woman looking at a trainer in a shoe shop. — Image caption,
Working out the original price will show you how much you are saving on a sale item.

VAT is a tax on what you spend. It is a percentage of the cost of an item or service. Some businesses can reclaim the VAT they pay on certain items. To do this, they have to reverse the percentage increase to calculate what they are owed. The rate of VAT in the UK is currently 20%.

When shopping for clothes or shoes in a sale, the price tag might show the cost after a percentage reduction. For example, the sale price of trainers is £46 following a discount of 20%. Working out the original price will show you exactly how much you are saving in the sale.

A white woman looking at a trainer in a shoe shop. — Image caption,
Working out the original price will show you how much you are saving on a sale item.

More on Percentages

Find out more by working through a topic

How to work out interest
count
7 of 7
What are percentages?
count
1 of 7
How to calculate percentages
count
2 of 7
How to find a percentage of an amount using bar models
count
3 of 7