Key points
A horizontalThe right-left direction on a graph or map. Parallel to the horizon. line is formed by coordinates with the same constantThe number or quantity that does not vary. Eg, in the equation 𝒚 = 3𝒙 + 6, the 3 and 6 are constants, where 𝒙 and 𝒚 are variables.
\(y\)-coordinate (\(x\), \(y\)). This is generalised by the equation \(y = c\), where \(c\) is the constant \(y\)-coordinate.A verticalThe up-down direction on a graph or map. line is formed by coordinates with the same constant \(x\)-coordinate
(\(x\), \(y\)). This is generalised by the equation \(x = c\), where \(c\) is the constant \(x\)-coordinate.The \(x\)𝒙-axisThe line on a graph that runs horizontally (left-right) through the origin. It is used as a reference to measure from. is a horizontal line with equation \(y = 0\). The \(y\)𝒚-axisThe line on a graph that runs vertically (up-down) through the origin. It is used as a reference to measure from. is a vertical line with equation \(x = 0\)
A line is continuous and extends forever. It has an infiniteUnlimited, endless length. When drawing a shape, each side is a line segmentA specific part of a line between two points..

Plotting horizontal and vertical lines
A horizontal line is made up of coordinateThe ordered pair of numbers (𝒙, 𝒚) that defines the position of a point. with a constant \(y\)-coordinate (\(c\)).The equation of the horizontal line is \(y = c\)
A vertical line is made up of coordinates with a constant \(x\)-coordinate (\(c\)).The equation of the vertical line is \(x = c\)
To draw the line \(y = c\):
- Find the constantThe number or quantity that does not vary. Eg, in the equation 𝒚 = 3𝒙 + 6, the 3 and 6 are constants, where 𝒙 and 𝒚 are variables. value \(c\) on the \(y\)-axis.
- Draw a horizontal line through the coordinates (0, \(c\)).
- Label the line with its equation.
To draw the line \(x = c\):
- Find the constant value \(c\) on the \(x\)-axis.
- Draw a vertical line through the coordinates (\(c\), 0).
- Label the line with its equation.
Examples
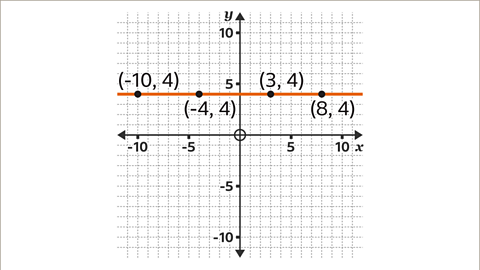
Image caption, A horizontal line is made up of coordinates with a constant 𝒚-coordinate.
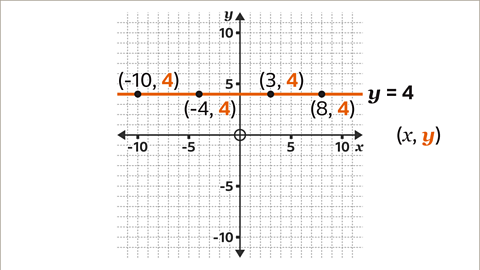
Image caption, Every coordinate on the line has a 𝒚-coordinate of 4. The constant is 4. The equation of the line is 𝒚 = 4
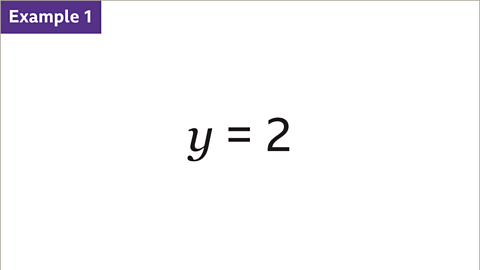
Image caption, Plot the line 𝒚 = 2
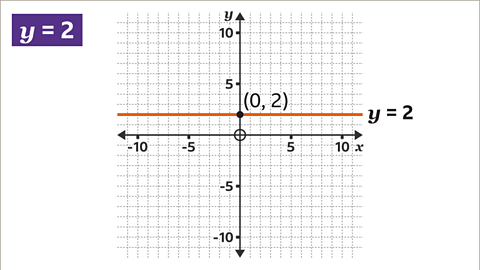
Image caption, Find the constant value (2) on the 𝒚-axis. Draw a horizontal line through the coordinates (0, 2). Label the line with its equation, 𝒚 = 2
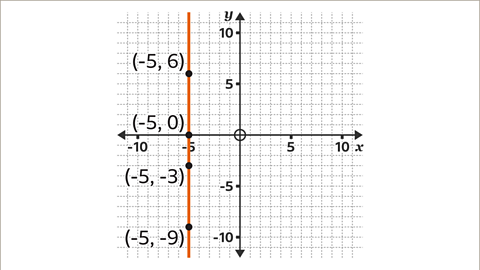
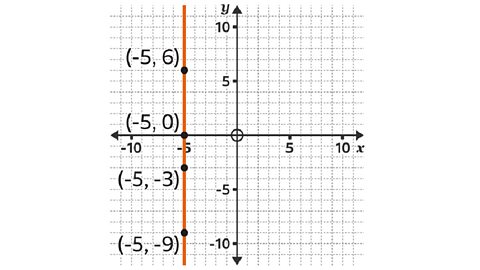
Image caption, A vertical line is made up of coordinates with a constant 𝒙-coordinate.
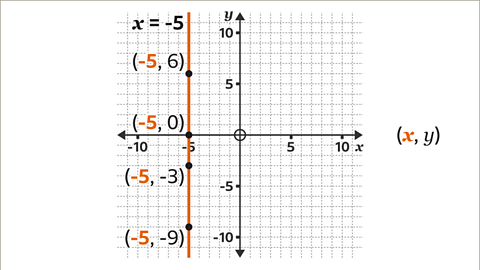
Image caption, Every coordinate on the line has an 𝒙-coordinate of -5. The constant is -5. The equation of the line is 𝒙 = -5
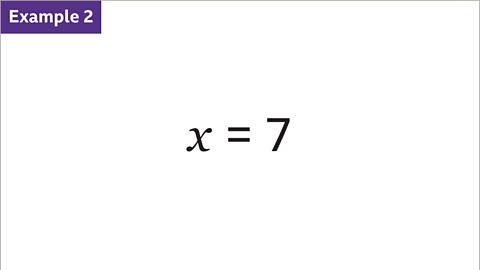
Image caption, Plot the line 𝒙 = 7
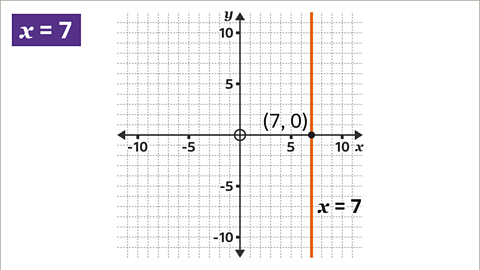
Image caption, Find the constant value (7) on the 𝒙-axis. Draw a vertical line through the coordinates (7, 0). Label the line with its equation, 𝒙 = 7
1 of 8
Question
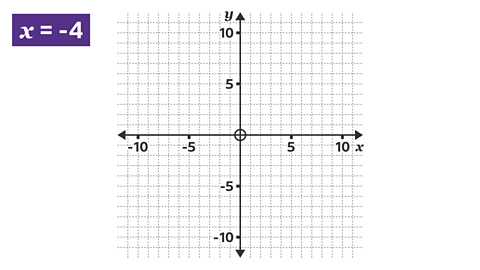
Draw the line \(x = -4\)
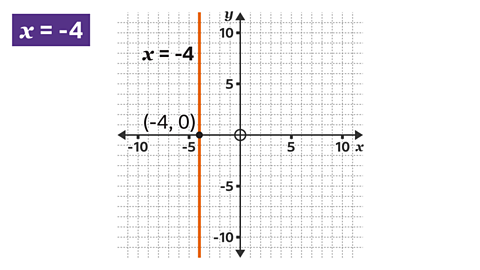
- Find the constant value (-4) on the \(x\)-axis.
- Draw a vertical line through the coordinates (-4, 0).
- Label the line with its equation, \(x = -4\)
Finding equations of horizontal and vertical lines
The equation of the \(x\)-axis is \(y = 0\)
The equation of the \(y\)-axis is \(x = 0\)
To find the equation of a horizontal line, or line segment:
- Extend the line to find the constant (\(c\)) at which it meets the \(y\)-axis.
- Label the line with the equation \(y = c\)
For a line segment, state the values of \(x\) for which the line segment is drawn.
To find the equation of a vertical line, or line segment:
- Extend the line to find the constant (\(c\)) at which it meets the \(x\)-axis.
- Label the line with the equation \(x = c\)
For a line segment, state the values of \(y\) for which the line segment is drawn.
Example
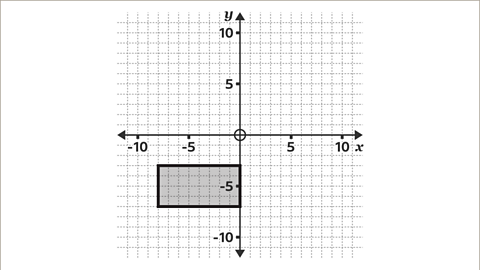
Image caption, Find the equations of each line segment that forms the rectangle.
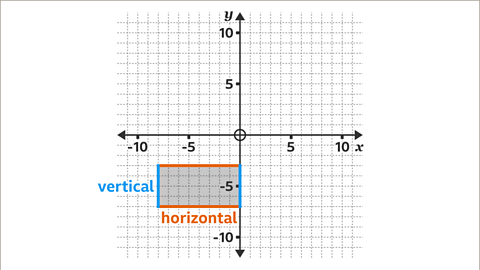
Image caption, The rectangle is drawn using two horizontal lines and two vertical lines.
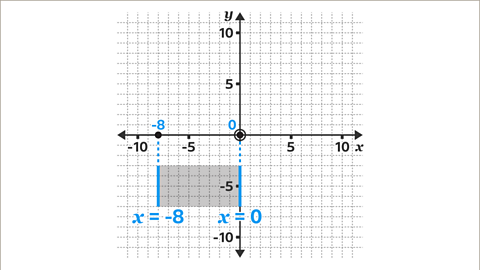
Image caption, Extend the vertical lines of the rectangle to meet the 𝒙-axis. One line meets the 𝒙-axis at -8. The equation of the line is 𝒙 = -8. The line segment for this side of the rectangle is 𝒙 = -8 for values of 𝒚 from -3 to -7. The other line meets the 𝒙-axis at 0. The equation of the line is 𝒙 = 0. The line segment for this side of the rectangle is 𝒙 = 0 for values of 𝒚 from -3 to -7
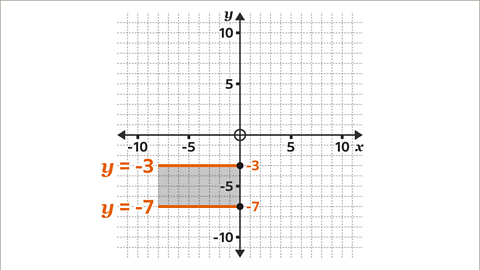
Image caption, Extend the horizontal lines of the rectangle to meet the 𝒚-axis (if needed). One line meets the 𝒚-axis at -3. The equation of the line is 𝒚 = -3. The line segment for this side of the rectangle is 𝒚 = -3 for values of 𝒙 from -8 to 0. The other line meets the 𝒚-axis at -7. The equation of the line is 𝒚 = -7. The line segment for this side of the rectangle is 𝒚 = -7 for values of 𝒙 from -8 to 0
1 of 4
Question
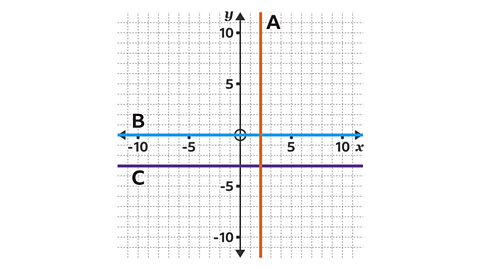
Give the equations of the three lines.
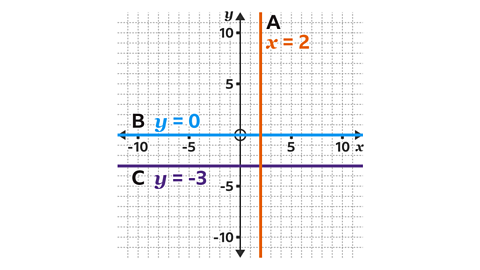
- Line A is vertical and crosses the \(x\)-axis at 2. The equation of line A is \(x = 2\)
- Line B is horizontal and crosses the \(y\)-axis at 0. The equation of line B is \(y = 0\), which is the equation of the \(x\)-axis.
- Line C is horizontal and crosses the \(y\)-axis at -3. The equation of line C is \(y = -3\)
Practise horizontal and vertical lines
Quiz
Practise plotting horizontal and vertical lines with this quiz. You may need a pen and paper to help you with your answers.
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Graphs
Find out more by working through a topic
- count4 of 7
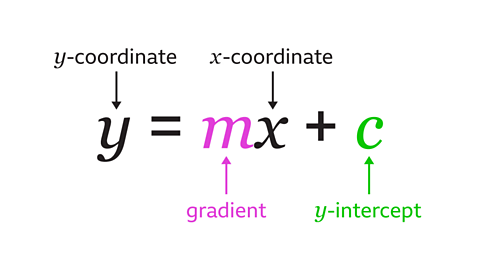
- count6 of 7
- count7 of 7