Box Plots

When data is presented as a list of numbers, it can be difficult to interpret.

If it is summarised in a diagram it is easier to draw conclusions and to compare with a different data set.

A box plot is a diagram which summaries the key features of a data set using just 5 key values.

These can be found easily once the values are arranged in order.

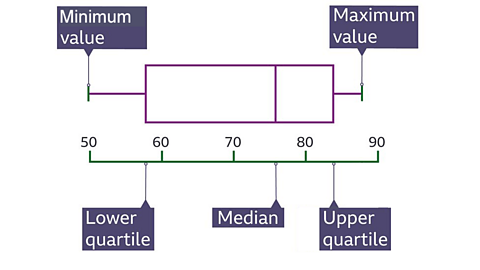
The 5 values to be identified are

• The minimum value – the smallest number in the data set

• The maximum value – the largest number in the data set

• The median - the middle value. 50% of the data is larger than this value and 50% of the data is smaller.

• The lower quartile is the value halfway between the minimum value and the median.

75% of the data is larger than this value and 25% is lower than this value .

• The upper quartile is the value half-way between the median and the maximum value.

25% of the data is larger than this value and 75% is lower than this value.

The ‘box’ has the lower quartile at one end and the upper quartile at the other.

The median is always somewhere inside the box. The height of the box is not important.

A box plot can be drawn from a data set using 5 key values.

Minimum, Maximum, Median, Lower Quartile and Upper Quartile.

Miss Fitt, the PE teacher, uses a spreadsheet to record the times taken for pupils to complete a cross country run.

She uses the sort function to arrange the times from fastest to slowest.

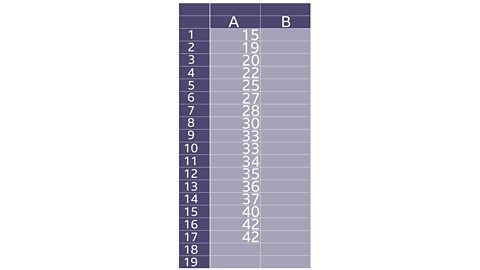
She wants to draw a box plot to show this data so first she needs to identify the 5 key values.

Minimum value = 15 minutes

Maximum value = 42 minutes

Median – There are 17 values so the median will be half-way - the 9th value which is 33 minutes

Lower Quartile – Half-way between the minimum and the median. This is the 5th value which is 25 minutes.

Upper Quartile – Half-way between the median and the maximum. This is the 13th value which is 36 minutes.

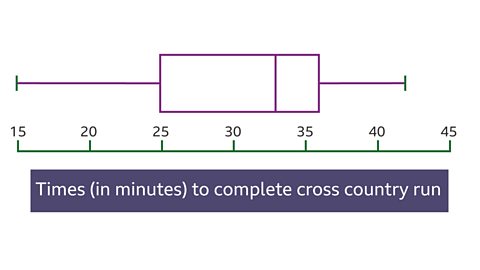
Miss Fitt uses the 5 values to draw the box plot below.