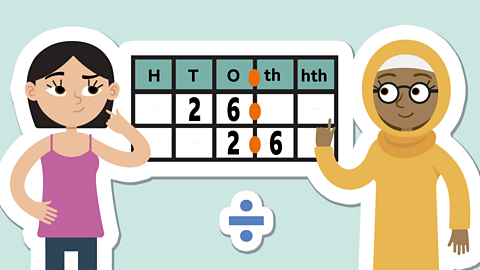
Multiplying three 1-digit numbers
The process of multiplying three numbers together is similar to the process of multiplying two numbers, but it has one extra step.
First, you multiply two of the numbers, then you multiply the third number by the product of the first two.
Multiplication can be done in any order. You can choose the easiest way of multiplying the three numbers together.

Quiz: Multiply three 1-digit numbers
Test out your knowledge of multiplying 3 single-digit numbers with this quiz, then read on to complete the page.
Multiplication using arrays
Here is an array. It shows 2 rows of 4 counters.
Or 4 counters multiplied by 2.
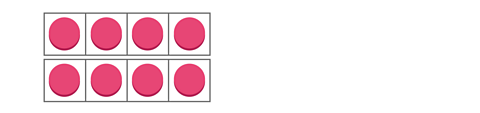
The multiplication sentence is:
4 × 2 = 8
Take a look at the next array. It shows 4 groups of 4 counters multiplied by 2.
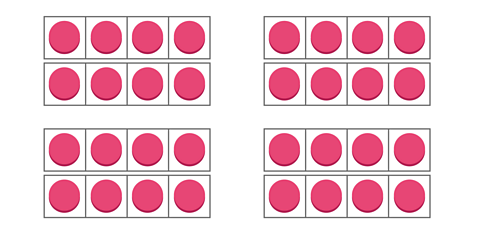
The multiplication sentence is:
4 × 4 × 2 = 32
Order of multiplication
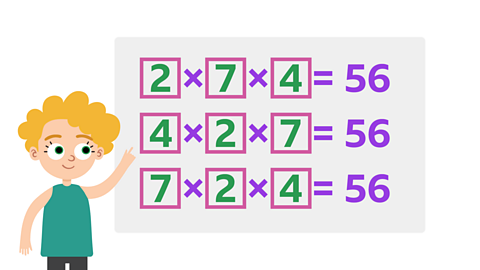
Here are 3 digit cards.

There are six different multiplication sentences that you can make from these three digits.
Explore those different multiplication sentences in this slideshow, to find out that the product is always the same.
This is because multiplication can be done in any order.
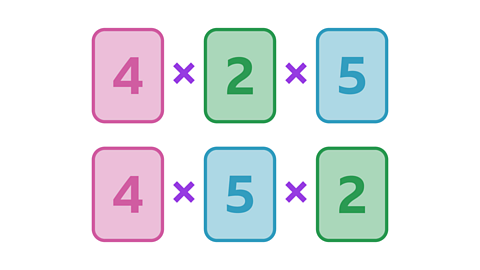
Image caption, These are two of the multiplication sentences that you can make from the cards.
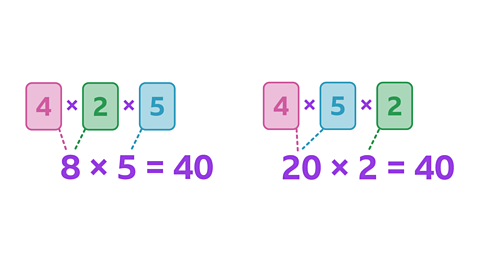
Image caption, The product of each calculation is 40.
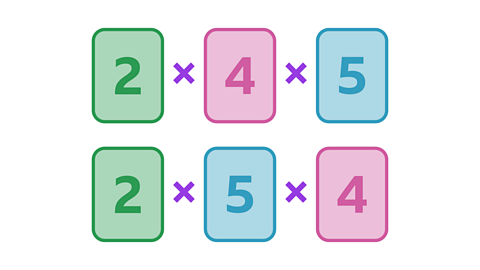
Image caption, Here are two more multiplication sentences that you can make from the three cards. What is the product of each calculation?
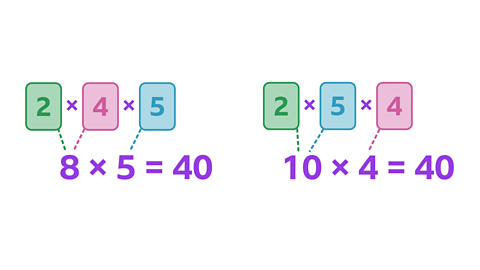
Image caption, The product is also 40 for these multiplication sentences.
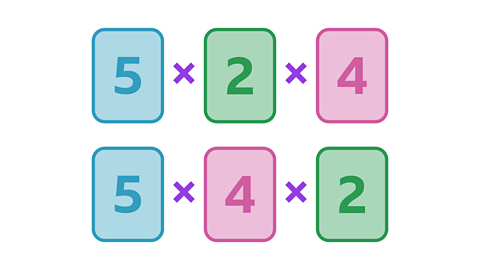
Image caption, Here are the final two multiplication sentences you can make.
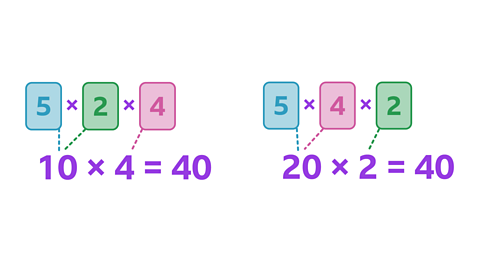
Image caption, The product is always 40.
1 of 6
You can decide which order to multiply the numbers in to make a calculation easier.
Look at the multiplication sentences below.
Which one is the easiest for you to calculate in your head?
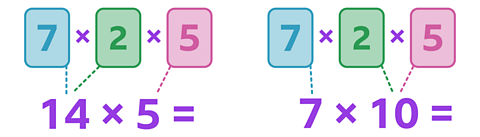
Looking at factors
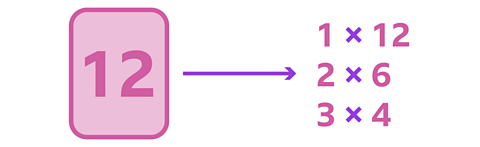
Factors are numbers that can be multiplied together to get another number.
For example, 12 is the product of these factors:
You can use what you know about factor pairs that make 12, to create a calculation that involves multiplying 3 digits together to make 12.
Let's think about how to create the calculation:

When you multiply a number by 1, the product is always the number you started with.
So, if you put a 1 in the first box, then you can use the factors of 12 to complete the other missing parts:
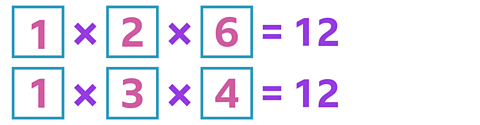
If you put 2 in the first box, then the other two numbers need to be factors of 6, because 2 x 6 = 12.
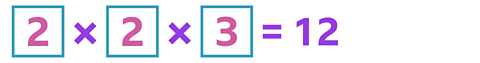
Don’t forget - you can change the order of the numbers because multiplication can be done in any order.
Example 1
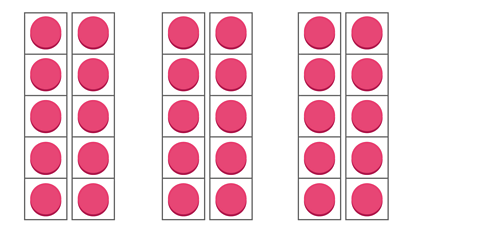
There are six different multiplication sentences, containing three factors, that can describe this array.
One of the sentences is:
2 × 5 × 3 = 30
Find five more sentences, containing three factors, that describe this array.
✓ The other 5 multiplication sentences are:
2 × 3 × 5 = 30
3 × 2 × 5 = 30
3 × 5 × 2 = 30
5 × 2 × 3 = 30
5 × 3 × 2 = 30
The product is always the same but the numbers in the multiplication sentences can be written in different orders.
Example 2
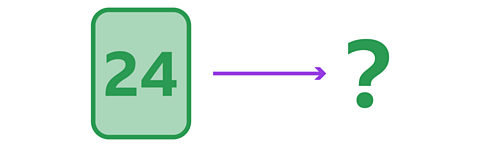
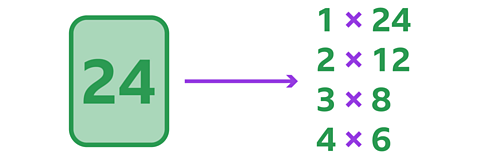
How many factors of 24 are there?
✓ There are 8 factors.
The factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.
Play our fun maths game Guardians: Defenders of Mathematica. gamePlay our fun maths game Guardians: Defenders of Mathematica
Use your times tables and more maths skills to defeat monsters and reclaim the Kingdom of Mathematica

More on Multiplying and dividing
Find out more by working through a topic
- count25 of 32

- count26 of 32

- count27 of 32

- count28 of 32