How to multiply decimals by integers

Whether you are calculating with addition, subtraction, multiplication or division, it is helpful to recognise the importance of:
- formal written methods (sometimes called standard written algorithms)
- efficient mental methods
When you multiply decimals by integers (whole numbers), you can use everything you already know about multiplying multi-digit numbers.

Quiz: Multiplying decimals by integers
Test out your knowledge of multiplying decimals by integers with this quiz, then read on to complete the page.
What methods can be used to multiply decimals by integers?
You can use written or mental methods to multiply decimals by whole numbers.
For written methods, you might choose to use the column method or the grid method.
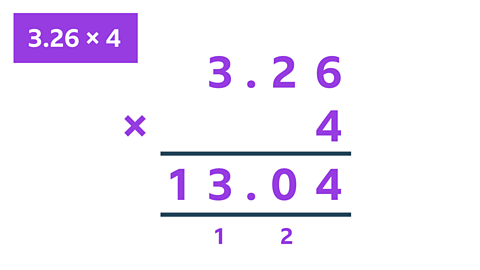
Image caption, Column method
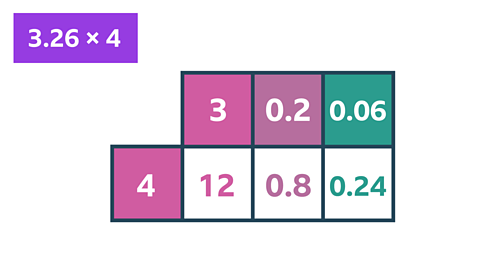
Image caption, Grid method
1 of 2
Using a mental method doesn’t mean you have to keep all the numbers in your head.
Many good mental methods involve making quick notes or writing down small steps to help you keep track of your calculations.
They can also help you understand the size and position of numbers in our number system.
To build your confidence, get plenty of regular practice with formal written methods. However, remember that sometimes a mental method can be quicker and just as effective.
How to use rounding to estimate decimal multiplication
You can use rounding to estimate the result of multiplying decimals by whole numbers.
This helps you quickly check if your final answer is reasonable.
Let’s look at this calculation:
8.7 × 6
8.7 lies between 8 and 9.
Here it is marked on a number line:
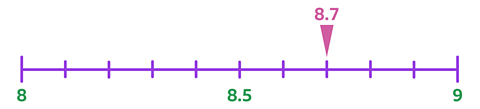
8.7 rounded to the nearest integer is 9.
So you can estimate that the answer would be between 48 (which is 8 × 6) and 54 (which is 9 × 6).
Now that you know an estimated answer, let's use other methods to find the correct answer.
You could use a formal written method for finding the answer to 8.7 × 6 the calculation as shown here:
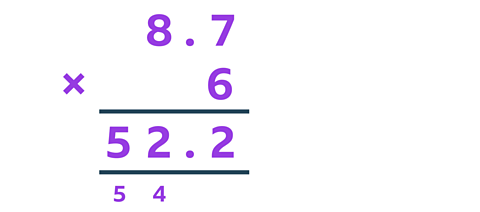
You could also use a mental method to calculate the answer:
To carry out the mental method, first partition the decimal number 8.7 into 8 and 0.7.
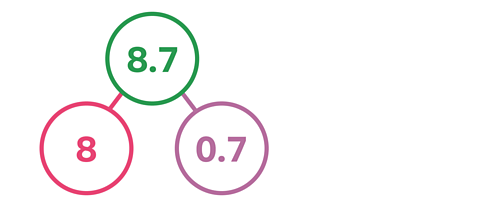
Then, multiply each part by 6.
8 × 6 = 48
0.7 × 6 = 4.2
The second calculation may look difficult at first, but you can calculate it by knowing that 0.7 × 6 is six lots of seven-tenths. That's 42 tenths or 4.2
You could also calculate 7 × 6 then divide the answer (which is 42) by 10 to get the figure 4.2.
Add the two products together to get the final answer.
48 + 4.2 = 52.2
How to multiply numbers by powers of ten
Understanding powers of ten can make multiplying numbers, especially decimals, much easier.
Let’s look at the calculation:
5.48 × 9
5.48 lies between 5 and 6.
Here it is on a number line:
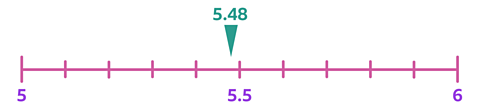
5.48 rounded to the nearest integer is 5 and 5.5 if rounded to one decimal place.
So you can estimate that the answer would be between 45 (which is 5 × 9) and 54 (which is 6 × 9).
Now that you know an estimated answer, let's use the column method to work out the correct answer.
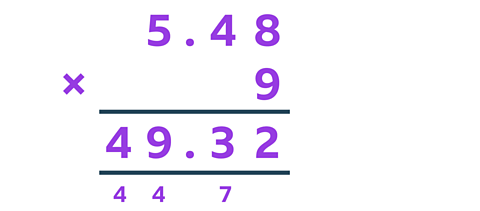
You could choose to solve this calculation mentally.
Multiplying 5.48 by 9 is like multiplying 10, but then subtracting one lot of 5.48.
It’s easy to multiply 5.48 by 10 in your head. The digits in the number move one place value column to the left.
5.48 × 10 = 54.8
Then you subtract one lot of 5.48 from the answer above.
54.8 - 5.48 = 49.32
Example 1
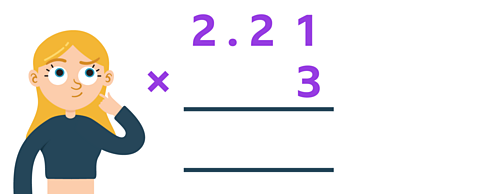
Work out 2.21 × 3
You could try using the column method, grid method or a mental method.
✓ The answer is 6.63.
Here is the working shown for the column method and grid method.
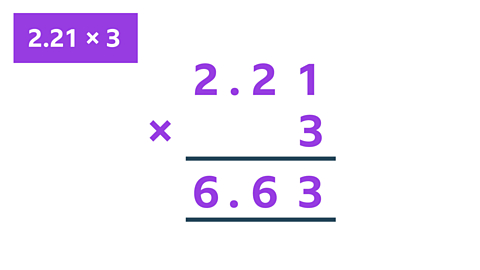
Image caption, Column method
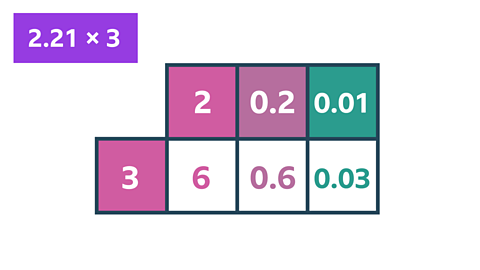
Image caption, Grid method
1 of 2
2.21 can be partitioned into 2, 0.2 and 0.01
Then you can work out these calculations separately.
2 × 3 = 6
0.2 × 3 = 0.6
0.01 × 3 = 0.03
Altogether that adds up to 6.63:
6 + 0.6 + 0.03 = 6.63
Which method did you use?
Example 2
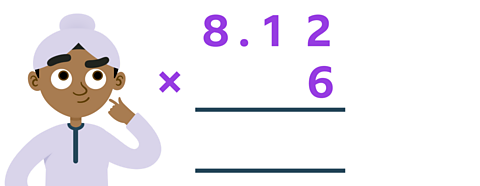
Work out 8.12 × 6
You can use whichever method works best for you.
✓ The answer is 48.72.
Which method did you choose?
This is how the column method can be used to find out the answer:
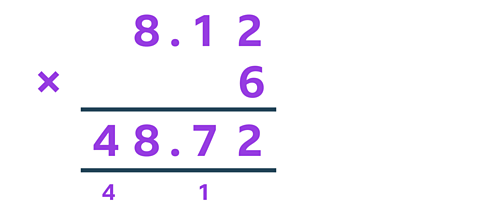
Example 3
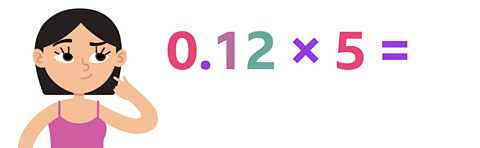
Work out 0.12 × 5
Try to use a mental method to work this calculation out, instead of a formal written method.
✓ The answer is 0.6.
Which method did you choose?
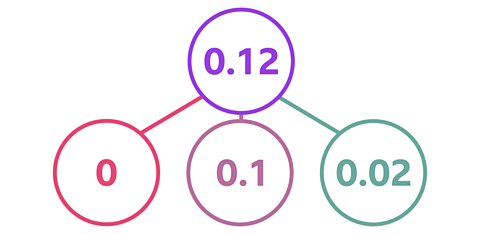
You could have partitioned 0.12 into 0.1 and 0.02.
0.1 × 5 = 0.5
0.02 × 5 = 0.1
0.5 + 0.1 = 0.6
Or you could have used your knowledge of powers of ten.
12 × 5 = 60
60 ÷ 100 = 0.6
Play our fun maths game Guardians: Defenders of Mathematica. gamePlay our fun maths game Guardians: Defenders of Mathematica
Use your times tables and more maths skills to defeat monsters and reclaim the Kingdom of Mathematica

More on Multiplying and dividing
Find out more by working through a topic
- count31 of 32

- count1 of 32

- count2 of 32
