Dividing decimals by 10, 100 and 1,000

When you divide a decimal by 10, 100 or 1,000, the place value of the digits decreases.
The number decreases in value by 10, 100 or 1,000 times.
The digits move to the right as the number gets smaller in value.
Remember, the decimal point does not move.

Quiz: Divide decimals by 10, 100 and 1,000
Test out your knowledge of dividing decimals by 10, 100 and 1,000 with this quiz, then read on to complete the page.
Decimals in daily life
Being able to divide decimals by 10, 100 or 100 can help you in everyday life.
Take a look at some examples:
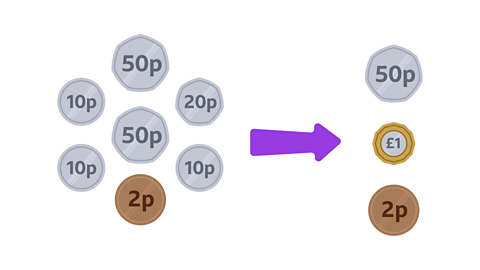
Image caption, Convert pounds to pence.
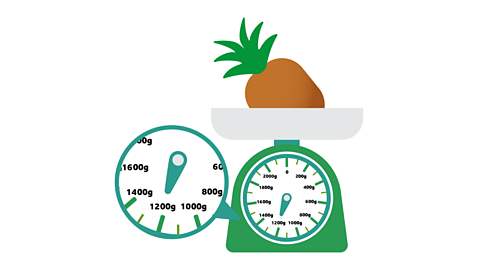
Image caption, Convert measures, such as grams to kilograms or litres to millilitres.

Image caption, Convert length, such as metres to centimetres or centimetres to millimetres.
1 of 3
Using a place value chart
You can use a place value chart to help you to divide by 10, 100 and 1,000. This helps you to see how the digits change in value.
A trick to help you remember how many places the digits need to move is to look at the zeros in 10, 100 and 1,000.
- ÷ 10 - there is 1 zero - move digits 1 place to the right
- ÷ 100 - there are 2 zeros - move digits 2 places to the right
- ÷ 1,000 - there are 3 zeros - move digits 3 places to the right
Let's take a look at a place value chart to see how the digits move one place to the right when dividing by 10.
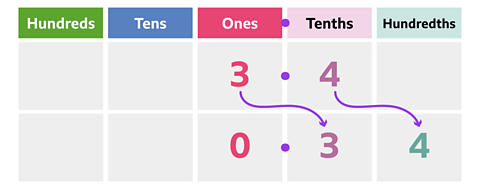
The calculation is:
3.4 ÷ 10 = 0.34
3 ones become 3 tenths. 4 tenths become 4 hundredths.
To divide by 100, you move the digits 2 places to the right. There are 2 zeros in 100.
The decimal point does not move.
Take a look at the next place value chart to see how the digits move two places to the right when dividing by 100.

The calculation is:
68 ÷ 100 = 0.68
6 tens become 6 tenths. 8 ones become 8 hundredths.
Don’t forget to add your decimal point and if there are no hundreds, tens or ones in your answer. Then add a 0 in front of the decimal point.
Finally, let’s see what happens when we divide 4,560 by 1,000.
There are 3 zeros in 1,000, so you need to move the digits 3 places to the right to divide by 1,000.
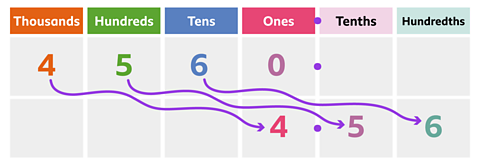
The calculation is:
4,560 ÷ 1,000 = 4.56
4 thousands become 4 ones. 5 tens become 5 tenths. 6 tens become 6 hundredths. 0 ones become 0 thousandths.
If there is a 0 at the end of a number, as there is in the example above, then once the 0 moves beyond the decimal point you no longer need to include it as it does not add any value to the number.
Remember, this is only if the 0 is at the end of the number.
Example 1

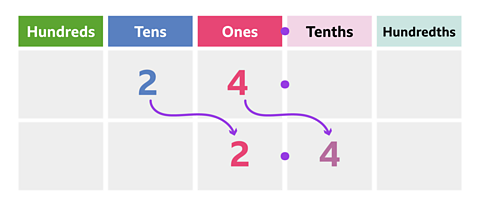
What is 24 ÷ 10?
✓ 24 ÷ 10 = 2.4
Look at the place value chart to see how the digits move one place to the right.
4 ones become 4 tenths. 2 tens become 2 ones.
You need to include a decimal point in the answer to show that the 4 ones are now 4 tenths.
The digits become ten times smaller in value and move right but the decimal point stays in the same position.
Example 2

Lucy has collected a mixture of pounds and pennies.
She has worked out that it's 723 pence altogether, but what is that amount in pounds?
✓ The amount in pounds is £7.23.
There are 100 pennies in a pound, so the calculation is:
723 ÷ 100 = 7.23
Can you see how each digit has moved two place values to the right?
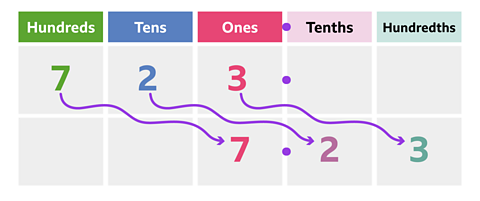
Example 3

Rohan has 3,465 millilitres of orange juice in two large jugs.
How many litre bottles will he be able to fill?
✓ He will be able to fill three litre-bottles.
There are 1,000 millilitres in a litre. So you should divide 3,465 by 1,000. He may have some juice that does not fill a whole litre bottle.
3,465 ÷ 1,000 = 3.465
He can fill three litre-bottles and will have 465ml left over.
More on Multiplying and dividing
Find out more by working through a topic
- count1 of 32

- count2 of 32

- count3 of 32
