Key points
speedA measure of how the distance travelled by a moving object changes with time. The average speed of a moving object is defined as the total distance travelled/time taken to travel that distance. The units of speed are length/time, eg kilometres per hour, or metres per second. is a compound measureMade up of more than one part. Eg, speed uses both distance and time and is a compound measure. linking distance and time.
Speed gives the distance travelled in a unit of time and measures how fast something is moving. The average speed is measured, as most objects do not move at a constantA number or quantity that does not vary. A constant speed is a steady speed. Eg, the speed of light is constant. The speed of a car is not constant, it varies. speed.
Units of speed are always a unit of length per unit of time.
Different units of length and time may be chosen depending on the situation. This makes it easier to read the measurements. For example, the speed a cricket ball travels might be measured in metres per second (m/s), while a car's speed might be measured in miles per hour (mph).
If two of the three variables – speed, distance or time – are known, the third can be worked out. A formula triangleA tool to help decide which calculation is needed to work out speed, distance, or time. can help solve a speed, distance or time problem.
Video
Watch the video to listen to Steph, a sports coach, describe how calculating speed, distance and time is useful when coaching and playing football.
Bobby: So, like on a day-to-day and a week-to-week basis, what does being a sports coach involve?
Steph: We train once a week for an hour. It’s important that we pick topics and focus on things for them to really learn. So, it might be passing, it might be shooting, it might be defending, or it might even be something like how you use speed to accelerate when we’re running with the ball to beat a defender.
Bobby: So, how will you try and incorporate speed into your training sessions?
Steph: So, we do a lot of work with the ball at our feet, so if you’re dribbling towards the defender, when might you use speed to go past them, to change direction, to fool them? And if you’re the defender, when might you try and really slow the player down so that the player running towards you doesn’t have a chance of beating you?
Bobby: So, as a maths teacher, I think of speed as the distance covered divided by the time. So, would you ever do a session where you’re running up and down the length of the pitch?
Steph: I wouldn't do that at my level but I think at higher levels, that happens a lot. One, for fitness training but also to work out howfast these players are. So, the higher you get up in football, the more important it is actually that you are able to accelerate, to decelerate and know when to do that at different moments in the game.
Bobby: And at the higher end elite levels of the game, are they still calculating speeds?
Steph: Oh, they’re definitely calculating speeds, far more than we are at the lower levels of the game. So, they might have a radar gun to do that, for example, or they might be using the equation that you just used. I know players coming for pre-season training, they're tested on their speed, they're tested that they hit a certain level and then they look to improve that with players all of the time.
Bobby: Brilliant. So how else might you use maths on a sort of basis outside of speed, distance and time?
Steph: At my level, I tend to just look at how many games players have played, what the score was, goals scored, assists and maybe how many times they were captain. But if you talk about the elite levels again, they're tracking absolutely everything.
What is speed and the units of speed?
Speed is a compound measureMade up of more than one part. Eg, speed uses both distance and time and is a compound measure. of how fast an object moves. It is given as a distance per unit of time.
Distances are units of length and can be given in metric unitsUnit of measurement in the metric system. Metric units include metre, centimetre, millimetre, kilometre. (including kilometres and metres) or imperial unitsA unit of measurement. Units include inch, foot, yard, and mile. Now largely replaced by metric units. (including miles and feet).
Units of time include hours, minutes and seconds.
Speed is stated as a length per unit of time. For example a speed could be 70 miles per hour, while another speed could be 45 metres per second.
Examples

Image caption, Speed is a compound measure of distance divided by time.

Image caption, Speed units are read as length unit per time unit. Units of speed include miles per hour (mph), kilometres per hour (km/h or kmph) and metres per second (m/s or ms⁻¹).

Image caption, Distance is a measure of length. Length can be given in metric units, such as kilometres, metres and centimetres, or imperial units, such as miles.

Image caption, The units of time include seconds, minutes, and hours.

Image caption, A car travelling 46 miles in one hour has an average speed of 46 miles per hour (46 mph).

Image caption, An athlete completing 100 metres in 10 seconds has an average speed of 10 metres per second (m/s). The athlete travels 10 metres every second.
1 of 6
How to use a formula triangle to find speed, distance or time
To calculate distance, speed or time given the other two variables:
Draw a formula triangleA tool to help decide which calculation is needed to work out speed, distance, or time. for speed, distance and time. Starting at the top and working clockwise, enter D for distance, T for time and S for speed.
Use the formula triangle to establish the correct calculation by covering up what needs to be worked out.
To work out speed, cover the S.
To work out distance, cover the D.
To work out time, cover the T.
The remaining variables show the calculation.
For speed, D over T means distance divided by time.
For distance, S and T next to each other means speed multiplied by time.
For time, D over S means distance divided by speed.
Substitute the values given and process the calculation. Write the answer with the correct units.
Examples
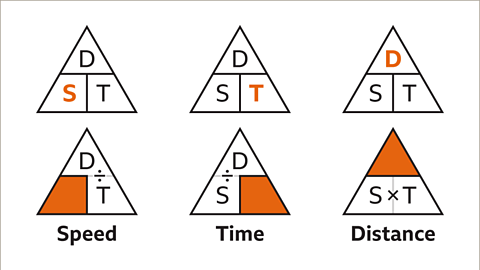
Image caption, When two variables are given the third can be calculated using the formula triangle.
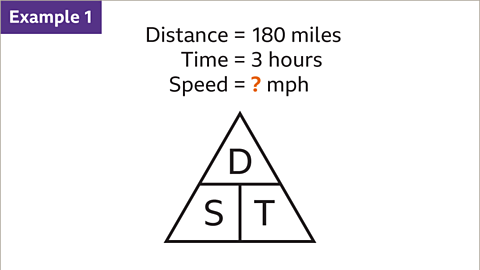
Image caption, A car journey of 180 miles takes 3 hours. Find the average speed of the car. Draw the formula triangle. Working clockwise from the top, enter D (distance), T (time) and S (speed).
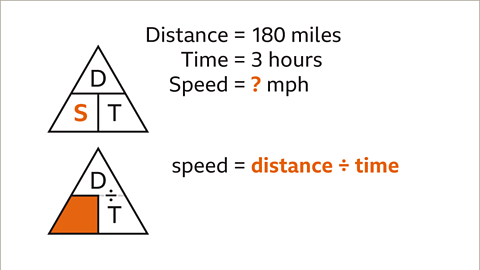
Image caption, To work out speed, cover up the S. The remaining variables are D over T. This means that to find the speed, the calculation is distance divided by time.

Image caption, Substitute the given values for distance (180) and time (3)
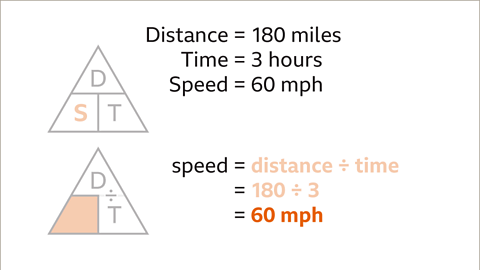
Image caption, Process the calculation (180 ÷ 3). Write the answer with the correct units (miles per hour). The average speed of the car is 60 mph.
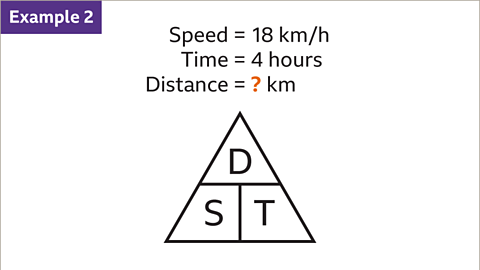
Image caption, A cyclist travels at an average speed of 18 km/h for 4 hours. Work out the total distance cycled. Draw the formula triangle. Working clockwise from the top, enter D (distance), T (time) and S (speed).
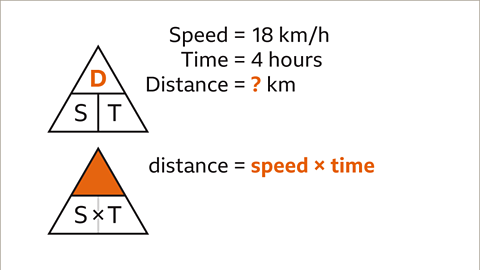
Image caption, To work out distance, cover up D. The remaining variables are S next to T. This means that to find the distance, the calculation is speed multiplied by time.
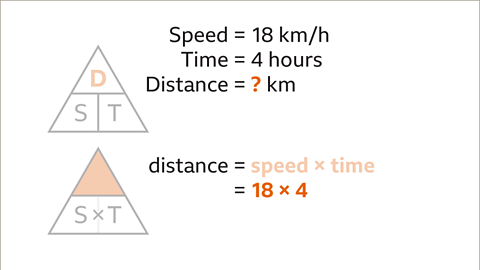
Image caption, Substitute the given values for speed (18) and time (4)
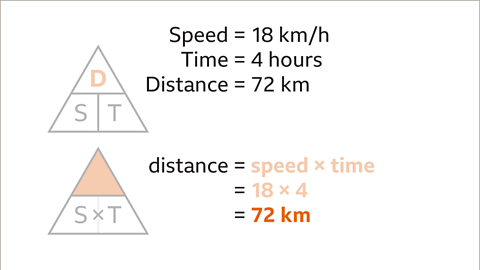
Image caption, Process the calculation (18 × 4). Write the answer with the correct units (kilometres/km). The distance cycled is 72 km.
1 of 9
Question
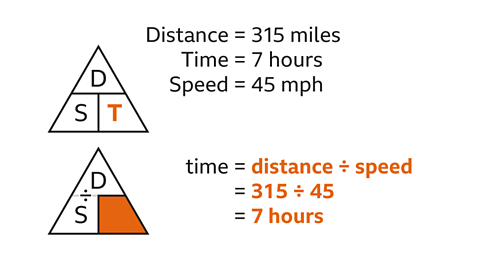
A car travelled 315 miles at an average speed of 45 mph. How long did it take?
Draw a formula triangle for speed, distance and time. Working clockwise from the top, enter D for distance, T for time and S for speed.
Use the formula triangle to work out the correct calculation.
Cover up T because time needs to be worked out. The remaining variables, D over S means distance divided by speed.
Substitute the values given, distance (315) and speed (45). Process the calculation (315 ÷ 45 = 7).
Write the answer with the correct units. The car took 7 hours to travel 315 miles at 45 mph.
Practise calculating speed, distance and time
Practise calculating speed, distance and time in this quiz.
Quiz
Real-world maths

In the early days of space exploration calculations were completed by ‘human computers’, such as Katherine Johnson.
This work included calculating speed, distance and time. Today, as then, these calculations are very important to plan and execute successful and safe space flights.
The actual calculations are more complex, and are only one part of the complicated maths involved.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Distance, speed and time
Find out more by working through a topic