Sequences
Number sequences are sets of numbers that follow a pattern or a rule.
Each number in a sequence is called a term.
A sequence which increases or decreases by the same amount each time is called a linear sequence.
It is useful to read the guides from M5 on sequences and from M1 on solving equations.
Position to term rule or nᵗʰ term
Each term in a sequence has a position. The first term is in position 1, the second term is in position 2 and so on.
Position to term rule is a formula which can be used to find any term in a sequence. This is also called the \(n^{th}\) term rule, in which \(n\) means any position in the sequence.
Example
Method 1
Work out the nᵗʰ term of the following sequence: 3, 5, 7, 9, …
Firstly, write out the sequence and the positions of the terms.
As there isn't a clear way of going from the position to the term, look for a common difference between the terms. In this case, there is a difference of 2 each time.
This common difference describes the times tables that the sequence is working in. In this sequence it's the 2 times tables.
Write out the 2 times tables and compare each term in the sequence to the 2 times tables.
| Position | 1 | 2 | 3 | 4 |
| Term | \(\times2\) | \(\times2\) | \(\times2\) | \(\times2\) |
| 2 times table | 2 | 4 | 6 | 8 |
| Operation | \(+1\) | \(+1\) | \(+1\) | \(+1\) |
| Term | 3 | 5 | 7 | 9 |
To get from the position to the term, first multiply the positions by 2 then add 1.
If the position is \(n\), then this is \(2\times n+1\) which can be written as \(2n+1\).
Method 2
Working out the nth rule
- Work out the common difference or term to term rule
- This gives the coefficient of \(n\)
- Work backwards from the first term to find the number that should be added or subtracted to find each term.
Example
Work out the \(n^{th}\) term for the following sequence: \(3, 5, 7, 9, …\)
Solution
- Work out the common difference or term to term rule.
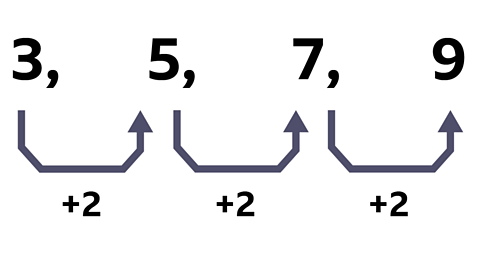
This gives the coefficient of \(n\), in this case 2.
The \(n^{th}\) term begins \(2n\).
- Work backwards from the first term to find the number that should be added or subtracted to find each term.
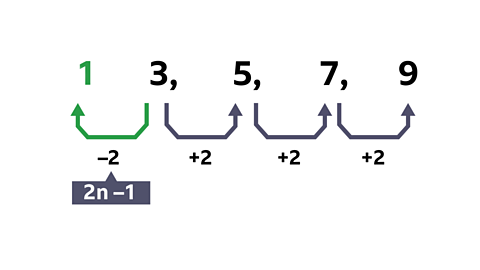
The \(n^{th}\) term for the sequence is \(2n – 2\).
Question
Work out the \(n^{th}\) term for the following sequence \(2, 5, 8, 11, …\)
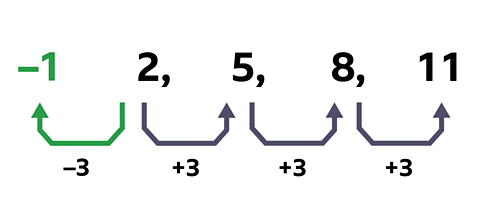
The \(n^{th}\) term for the sequence is \(3n – 1\).
Using the nᵗʰ term
If the nᵗʰ term of a sequence is known, it is possible to work out any number in that sequence.
Example
Write the first five terms of the sequence \(3n+4\).
\(n\) represents the position in the sequence. The first term in the sequence is when \(n=1\), the second term in the sequence is when \(n=2\), and so on.
To find the terms, substitute \(n\) for the position number:
- when \(n=1,3n+4=3\times1+4=3+4=7\)
- when \(n=2,3n+4=3\times2+4=6+4=10\)
- when \(n=3,3n+4=3\times3+4=9+4=13\)
- when \(n=4,3n+4=3\times4+4=12+4=16\)
- when \(n=5,3n+4=3\times5+4=15+4=19\)
The first five terms of the sequence: \(3n+4\) are \(7, 10, 13, 16, 19, …\)
Working out terms in a sequence
When the n
Question
What is the 100th term in the sequence \(5n–3\)?
To answer this, the position is 100, so substitute \(n\) for 100.
\(5n – 3 = 5\times 100 – 3 = 500 – 3 = 497\)
497 is the 100\(^{th}\) term in the sequence \(5n – 3\).
Is the number 14 in the sequence \(4n+2\)?
To work out whether 14 is in this sequence, put the nth term equal to the number and solve the equation.
\(4n + 2 = 14\)
\(–2\) \(–2\)
\(4n = 12\)
\(\div4\) \(\div4\)
\(n = 3\)
This means that 14 is in the sequence and it is the third term.
More on M6: Number
Find out more by working through a topic
- count1 of 2
