Problem 1 - Books and magazines
Problem 1 is all about working out how many books there are in different boxes.
Maths teacher Chris Smith and pupils from Grange Academy are here to explain.
The Maths Week Scotland Daily Challenges have been set by the Scottish Mathematical Council.
CHRIS: This problem is about working out how many books there are in different boxes.
Eilidh is a second hand bookseller and she needs to clear some space in her shop. She has six boxes of books and a box of magazine she wants to move.
Each box shows how many items there are in it.
Eilidh makes the space she needs by selling off some books to one customer, twice that number to another customer and keeping the magazines for herself.
Can you work out how many magazines Eilidh held on to?
One book buyer is gonna get twice as many books as the other person. Yeah? So think about what that might tell you, anybody got any ideas what that tells us?
PUPIL: What can you work out about the total number of books?
CHRIS: So you'd need a thirty one. Can you make 31 from the numbers that are available?
PUPIL: Can you find out how many books each customer buys?
CHRIS: Every one book he's got, you've got two books, yeah?
PUPIL: Can you find different totals from adding different boxes together?
CHRIS: So that's a useful thing to know, though.
The amount of books in one pile has got to be double the amount of books in the other pile.
PUPIL: Good luck everyone and try your hardest.
So here's the challenge:
Eilidh is a second-hand bookseller and she needs to clear some space in her shop.
She has six boxes of books and one box of magazines she wants to move.
Each box shows how many items there are in it. The boxes hold 24, 19, 17, 20, 25, 16 and 16 items.

Eilidh makes the space she needs by:
- selling off some books to one customer
- twice that number to another customer
- keeping the magazines for herself
Can you work out how many magazines Eilidh held on to?
Need a hint?
- What can you work out about the total number of books?
- Can you work out how many books each customer buys?
- Can you find different totals by adding different boxes together?
Solution
Worked out the answer? Here's how you can do it.
Did you manage to divide up Eilidh's boxes and find out how many magazines she kept?
Here's one way you could have solved it.
There are seven boxes in total, one of them contains magazines so the other six all contain books.
Since the books can be divided so that one customer gets twice as many as the other, the total number of books must be a multiple of three.
One person's getting double the amount of the other person.
So altogether that's gonna add up to, like, a multiple of three books.
Love it. Love it!
To solve this problem, let's find the total number of all the books plus magazines.
So add all the numbers together: 16 plus 20 plus 19 plus 24 plus 17 plus 25 plus 16 which equals 137. If you divide 137 by 3, you're left with a remainder of two. The total number of books is a multiple of three, so that means that the number of magazines in the box you remove must also have a remainder of two when you divide by three.
Divide each number by the three.
Most of the numbers don't work.
The only ones that do are twenty, because twenty divided by three is six remainder two, and seventeen, because seventeen divided by three is five remainder two.
Now try removing each number from the total, 137.
If we remove twenty we're left with one hundred and seventeen. One hundred and seventeen divided by three is thirty nine, but no combination of the remaining books gives thirty nine so it can't be that one.
If we remove seventeen, we're left with one hundred and twenty. One hundred and twenty divided by three is forty.
It looks like Eilidh kept the box with seventeen magazines in it but let's check.
We can get to forty books by adding together the box with sixteen items and the box with twenty four items and the other customer gets twice that number: eighty books. And sure enough the remaining boxes, twenty plus nineteen plus twenty five plus sixteen, add up to eighty, so that confirms the answer that Eilidh keeps the box with seventeen magazines in it.
Well done if you worked that out.

One customer buys twice as many books as the other. Between the two customers they buy three times a certain number of books.
The total number of books must be a multiple of three, so that it divides by three to give a whole number.


Step 1
Find the total number of books and magazines:
16 + 20 + 19 + 24 + 17 + 25 + 16 = 137
Step 2
Divide the total by three:
137 ÷ 3 = 45 remainder 2
We know that the total number of books is a multiple of three. This means if the number of magazines is divided by three it would also leave a remainder of two.

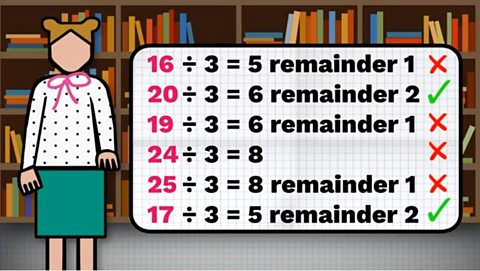
Step 3
Divide each number by three to see which leaves a remainder of two:
16 ÷ 3 = 5 remainder 1
20 ÷ 3 = 6 remainder 2
19 ÷ 3 = 6 remainder 1
24 ÷ 3 = 8
25 ÷ 3 = 8 remainder 1
17 ÷ 3 = 5 remainder 2
There are only two possible numbers of magazines: 20 or 17.
Step 4
Try removing each number from the total:
137 - 20 =117
137 - 17 = 120
When you divide the answer by three, that should tell us the number of books the first customer bought
117 ÷ 3 = 39
120 ÷ 3 = 40
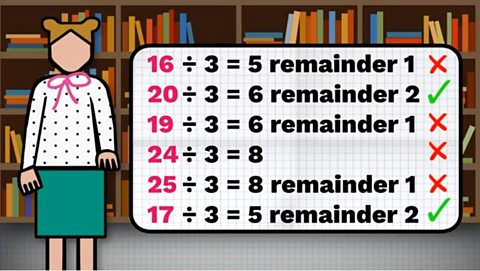

Step 5
Check and see if you can make this number by adding together boxes.
The remaining boxes have 24, 19, 17, 25, 16 and 16 items.
None of these can add together to make 39.
This means Eilidh did not keep 20 magazines.


But 16 +24 = 40
and 20 + 19 + 25 + 16 = 80, which is 2 x 40.
This fits with the information that the second customer bought twice as many books as the first customer.
So this confirms the answer:Eilidh kept 17 magazines.

Maths Week Scotland 2023. listMaths Week Scotland 2023
Try out all the daily challenges from Maths Week Scotland 2023.

Maths Week Scotland 2022. listMaths Week Scotland 2022
Try out all the daily challenges from Maths Week Scotland 2022.

Maths Week Scotland 2021. listMaths Week Scotland 2021
Want more maths challenges? Here are all the problems from 2021.

More on Problem solving
Find out more by working through a topic
- count2 of 21

- count3 of 21

- count4 of 21

- count5 of 21
