How to add and subtract fractions

There are two rules to remember when adding or subtracting fractions.
The fractions need to have a common denominator. This means the denominator has to be the same.
You only need to add or subtract the numerators.

Activity: Adding and subtracting fractions
Complete this interactive activity to understand how to add and subtract fractions. Then put your knowledge to the test.
How to add fractions
When adding fractions, make sure the denominator is the same.
The denominator is the number written below the division line on a fraction. It shows the total number of equal parts the whole is divided into.
Let's look at adding fractions first.
\(\frac {3} {6}\) + \(\frac {2} {6}\) = ?
This circle has been divided into 6 equal parts and \(\frac {3} {6}\) and \(\frac {2} {6}\) shaded.
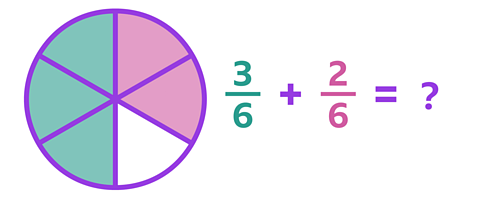
To add \(\frac {3} {6}\) and \(\frac {2} {6}\), count the number of one sixths that have been shaded in total. The answer is \(\frac {5} {6}\).
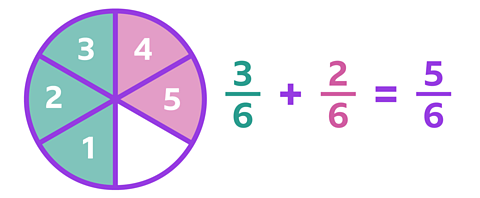
You only add the numerators together. The denominator always stays the same, because that is the number of parts the circle is divided into, and this has not changed.
How to subtract fractions
When subtracting fractions, the denominators still needs to be the same before you start the calculation.
This time, subtract one numerator from the other.
Let's look at a subtraction calculation:
\(\frac {6} {8}\) - \(\frac {2} {8}\) = ?
This bar model has been divided into 8 equal parts and \(\frac {6} {8}\) has been shaded.
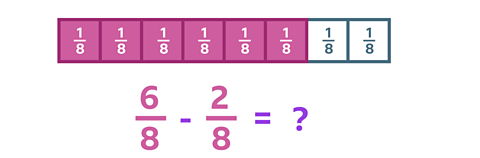
If you take away \(\frac {2} {8}\) from \(\frac {6} {8}\) that are shaded, you can see that there are \(\frac {4} {8}\) left.
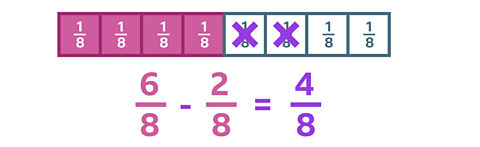
Looking at the calculation, you can see that you only need to subtract one numerator from the other. The denominator stays the same.
Example 1

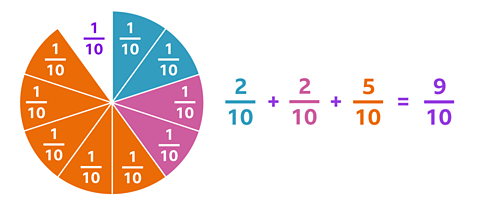
An orange has been cut into 10 equal pieces.
James eats two pieces, Lucas eats two pieces and John eats five pieces.
What fraction of the orange has been eaten?
You can use the diagram to help you work out the answer.
✓ \(\frac {9} {10}\) of the orange has been eaten.
Example 2
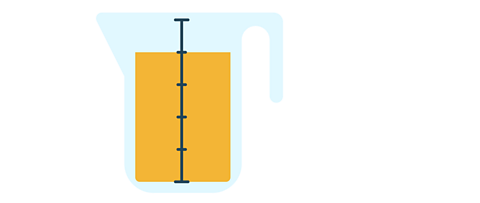
Here is some juice in a jug. There is \(\frac {4} {5}\) of it left.
If you drank \(\frac {2} {5}\) of it, how much would be left?
✓ There would be \(\frac {2} {5}\) left.
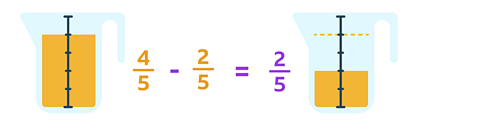
Example 3

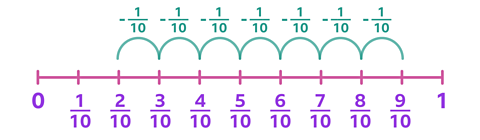
Use the numberline to work out this calculation:
\(\frac {9} {10}\) - \(\frac {7} {10}\) =
✓ The answer is \(\frac {2} {10}\).
Put your finger on \(\frac {9} {10}\), then move your finger back 7 tenths on the number line to find the answer.
Play our fun maths game Guardians: Defenders of Mathematica. gamePlay our fun maths game Guardians: Defenders of Mathematica
Use your times tables and more maths skills to defeat monsters and reclaim the Kingdom of Mathematica

More on Fractions
Find out more by working through a topic
- count1 of 5

- count2 of 5
- count3 of 5

- count4 of 5
