Key points about ratio and fractions, and sharing in a ratio

- A ratioA ratio compares two or more quantities by using parts of a whole, eg a ratio of 1 : 5 means that for every 1 of the parts on the left, there are 5 of the parts on the right. shows the relationship between two or more parts.
- Each part of a ratio, eg 3 : 4, can be shown as a fraction of a whole.
- An amount can be shared in a ratio by finding the value of each part.
- bar modelA diagram using rectangles to visualise how an amount can be shared. diagrams are used to represent ratios and fractions visually in order to solve problems, such as dividing amounts in a given ratio.
To be confident with this topic, make sure you have an understanding of ratio and can calculate with fractions.
Video – Dividing into a given ratio
Watch this video to learn how to use bar models to divide amounts in a given ratio, with worked examples.
Dividing into a given ratio.
You can use bar models to divide amounts in a given ratio.
For example, Isabel and Geraint share their savings of £96 in the ratio 5 to 3.
How much money does each person get?
First, let's work out how many parts there are in total.
Isabel gets 5 parts and Geraint gets 3 parts. 5 add 3 equals 8 parts in total. This means the total amount, £96, is split into 8 parts. £96 divided by 8 equals £12, so each part represents £12.
Isabel will get 5 of these parts, so £12 multiplied by 5 equals £60.
And Geraint will get 3 of these parts, so £12 multiplied by 3 equals £36.
To check your answer, add the two shares. £60 add £36 equals £96, which is the correct total.
Let's try another question.
Malcolm, Jamal and Aoife are given £72.90. They agree to share it in the ratio 2 to 4 to 3. How much money does each person get?
This time, the money is being split between three people and the total number of parts is 2 add 4 add 3, which equals 9.
So, divide the total £72.90 by 9 to find that each part represents £8.10.
Malcolm gets 2 parts, so that's £8.10 multiplied by 2, which equals £16.20.
Jamal gets 4 parts, so that's £8.10 multiplied by 4, which equals £32.40.
And Aoife gets 3 parts, so that's £8.10 multiplied by 3, which equals £24.30.
To check your answer, add these values together.
This equals £72.90 which is the correct total.
Check your understanding
Ratio and fractions
A ratio shows the relationship between two or more parts.
A fraction shows the relationship between a part and the whole.

- The ratio of blue to orange parts is 2 : 3.
For every 2 blue parts, there are 3 orange. - The fraction that is blue is \(\frac{2}{5}\).
2 parts out of a total of 5 are blue. - The fraction that is orange is \(\frac{3}{5}\).
3 parts out of a total of 5 are orange.

To form fractions from a ratio, the part being referred to becomes the numeratorNumber written at the top of a fraction. The numerator is the number of parts used, eg for ⅓, the numerator is 1., and the total of the parts becomes the denominatorNumber written on the bottom of a fraction. The denominator is the number of equal parts, eg for ⅓, the denominator is 3..
Problem solving with ratios and fractions can also include percentages as another way of writing parts of a whole.

Remember
63% means 63 parts out of 100, which is \(\frac{63}{100}\) as a fraction.
Follow the working out below
GCSE exam-style questions

- The number of large to small lockers at a swimming pool is 5 : 1.
All the large lockers and a quarter of the small lockers are full.
What fraction of all the lockers are full?
Write your answer in simplest form.
\(\frac{7}{8}\)
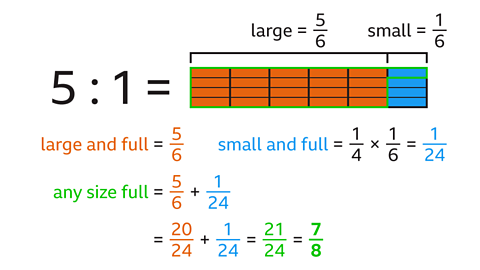
- Find the fraction of lockers that are each size.
There are 6 parts altogether in the ratio 5 : 1.
\(\frac{5}{6}\) are large and \(\frac{1}{6}\) are small. - Find the fraction of lockers that are small and full.
This is a quarter of \(\frac{1}{6}\). - Calculate \(\frac{1}{4}\) × \(\frac{1}{6}\) = \(\frac{1}{24}\).
- Add the fraction of large full lockers (\(\frac{5}{6}\)) and the fraction of small full lockers (\(\frac{1}{24}\)).
Make both the denominators equal to 24 by multiplying the top and bottom of \(\frac{5}{6}\) by 4.
\(\frac{5}{6}\) + \(\frac{1}{24}\) = \(\frac{20}{24}\) + \(\frac{1}{24}\) = \(\frac{21}{24}\) - Simplify\(\frac{21}{24}\) by dividing the numerator and denominator by 3.
The fraction of full lockers is \(\frac{7}{8}\).
- There are 10 times more right-handed students than left-handed students in a class.
What fraction of the class are left-handed?
\(\frac{1}{11}\)
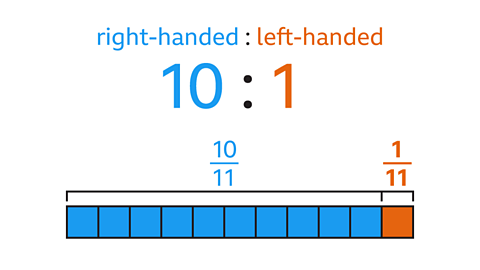
The ratio of right-handed to left-handed students is
10 : 1.
There are 10 + 1 = 11 parts in total.
1 out of 11 students is left-handed.
- A fruit salad contains apples and grapes in the ratio
2 : 3. The ratio of green grapes to red grapes is
1 : 3.
What percentage of all the fruit is green grapes?
15%
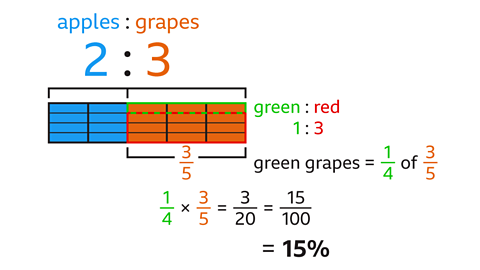
- From the ratio 2 : 3, the fraction of the salad that is grapes is \(\frac{3}{5}\).
- From the ratio 1 : 3, of all the grapes, the fraction that are green is \(\frac{1}{4}\).
The fraction of the salad that is green grapes is \(\frac{1}{4}\) of \(\frac{3}{5}\). - Multiply the two fractions to give \(\frac{3}{20}\).
- Convert to a percentage by finding an equivalent fraction with a denominator of 100.
Multiply the numerator and denominator by 5.
\(\frac{3}{20}\) is equivalent to \(\frac{15}{100}\), which is 15%.
Game - Ratio with other proportions
Complete this puzzle on ratio with other proportions from the Divided Islands game.
Play the full Divided Islands game.
Ratios as fractions – interactive activity
This interactive activity will help you understand how to form fractions from a ratio of two or three values.
Sharing in a ratio
Lots of things in everyday life are shared in ratios. Money is shared, drinks are mixed and members of teams are assigned using ratios.
To share a given quantity in a ratio:
- Find the total number of parts by adding the parts of the ratio.
- Divide the whole quantity by the total number of parts to find the value of one part.
- Multiply the value of one part by the number of parts needed.
A bar modelA diagram using rectangles to visualise how an amount can be shared. can illustrate the sharing of a quantity into parts.
Follow the working out below
GCSE exam-style questions

- Angle A and B form a straight line.
Angle B is 4 times bigger than angle A.
What is the size of angle B?
144°
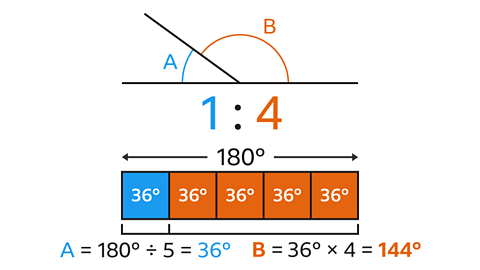
- The ratio of A to B is 1 : 4.
- There are 1 + 4 = 5 parts in total.
- The total is worth 180° as angles on a straight line add up to 180°.
- Divide 180° by 5 to find the value of each part.
- Each part is 36°.
- Angle B is 4 parts.
- Multiply 36° by 4 to give B = 144°.
- Fin wants to make 360 g of cookie dough.
The recipe uses flour, butter and sugar in the ratio
2 : 1 : 3. They have 140 g of flour, 100 g of butter and 160 g of sugar.
Do they have enough of each ingredient?
No, Fin doesn’t have enough sugar.

- Share 360 g in the ratio 2 : 1 : 3.
- There are 2 + 1 + 3 = 6 parts in total.
- Divide 360 g by 6 to find the value of each part.
- Each part is 60 g.
- Find how much of each ingredient they need.
- They need 2 parts flour: 2 × 60 g = 120 g.
- They need 1 part butter: 60 g.
- They need 3 parts sugar: 3 × 60 g = 180 g.
- Compare the values Fin needs with the amounts they have.
They have enough flour and butter, but are 20 g short of sugar.
- In an earring collection, \(\frac{1}{7}\) are gold.
Silver and blue are in the ratio 1 : 2.
There are 56 earrings in total.
How many are blue?
32 earrings are blue.
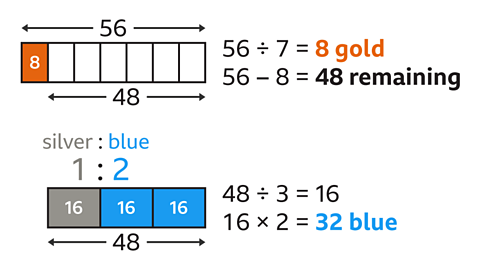
- \(\frac{1}{7}\) of 56 is 56 ÷ 7 = 8 gold earrings.
- There are 56 - 8 = 48 earrings remaining to share in the ratio 1 : 2
- Find the total number of parts in the ratio 1 : 2.
There are 1 + 2 = 3 parts in total. - Divide 48 by 3 to find the value of each part.
- Each part is 16.
- There are 2 parts blue.
16 × 2 = 32 blue earrings.
Game - Sharing in a ratio
Have a go at these puzzles on sharing in a ratio from our Divided Islands maths game.
Play the full Divided Islands game.
Video – Exam practice: Calculating ratios
Watch this video to learn how to calculate ratios and find out why it is important to work out the value of one part of a ratio.
Have you ever shared a pizza with friends, or followed a recipe? Then you've already used ratios.
They're everywhere in real life and they're likely to pop up in your exams too. So, how do we calculate ratios? Let's imagine a big family dinner.
There's delicious curry or tasty pasta on the menu. The ratio of people choosing curry to pasta is 8 : 5. So for every 8 curry fans, there are 5 pasta lovers. We also know that 6 more people would like to eat curry.
How do we calculate how many people are choosing pasta? Let's put this all together.
Ratios are made up of parts and in our family dinner, 8 parts of the family are having curry, while 5 parts are tucking into pasta. The key to answering this question is to look at the differences between the two parts of the ratio. So that's 8 parts for curry subtract 5 parts for pasta. 8 - 5 = 3 parts of our ratio. We know these 3 parts represent the 6 extra people who chose curry.
To calculate 1 part of the ratio, we divide 6 by 3, which equals 2. So 1 part of the ratio stands for 2 people. Now, to find how many people chose pasta, we simply multiply the 5 parts for pasta by 2.
5 × 2 = 10 people. Therefore, 10 people are choosing to enjoy a plate of pasta.
By working out the value of one part of a ratio, you can solve any ratio problem that comes your way.
Quiz – Ratio and fractions, and sharing in a ratio
Practise what you've learned about ratios and fractions, and sharing in a ratio with this quiz.
The questions change each time you try, so keep testing your knowledge.
Now that you have revised ratio and fractions, and sharing in a ratio, why not look at what are fractions?
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Ratio, proportion and rates of change
Find out more by working through a topic
- count3 of 8
- count4 of 8
- count5 of 8




