Nets of 3D shapes

Part ofMaths2D shapesYear 6

What is a net?

The net of a 3D shape is what it looks like if it is opened out flat.

There are many types of nets for the different 3D shapes.

A net is made from polygons that can be folded and joined to make a polyhedron.

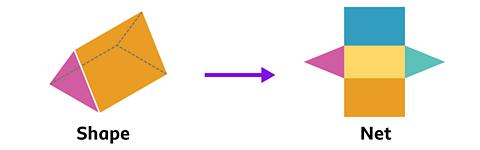
Here is the net of a triangular prism.

A triangular prism next to its unfolded net. The triangular prism has 2 triangular faces and 3 rectangular faces. The net has 2 triangles and 3 rectangles. The triangles are attached either side of the central rectangle.
Back to top

Quiz: Nets of 3D shapes

Why not see how much you know about this topic already? Then complete the page and see if you can beat your score.

Back to top

Polygons and polyhedrons

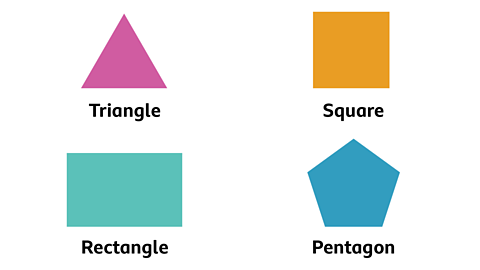
A polygon is a flat shape with straight sides.

Triangles, squares, rectangles and pentagons are examples of polygons.

A triangle, square, rectangle and pentagon.

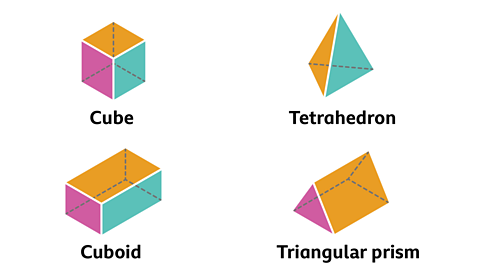
A polyhedron is a 3D shape with faces made from polygons.

Cubes, cuboids, tetrahedron and prisms are examples of polyhedra.

A cube, cuboid, tetrahedron and triangular prism.

When you open out a polyhedron as a net, it shows all the polygons that it is made from.

For example here is the net of a cuboid.

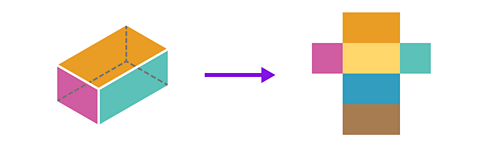
A net of a cuboid with 6 rectangles. The rectangles are in a pattern that can be folded into a cuboid shape.
Back to top

Nets of cubes

A cube is a 3D shape with 6 square faces.

Skip image gallery
  1. A cube.

    Click quickly through the slides to see how it can open out into a net.

If the net is closed up again, it can open into a different net.

Skip image gallery
  1. The net of a cuboid fully opened and flat. It's shaped like a lower case 't'.

    Click through the slides quickly to see the net of the cube close up and open up again.

There may be several possible nets for one 3D shape.

Back to top

Nets of 3D shapes

The nets of 3D shapes help you see some of the properties of the shape.

This net of a tetrahedron shows you the shape of each face and the number of faces.

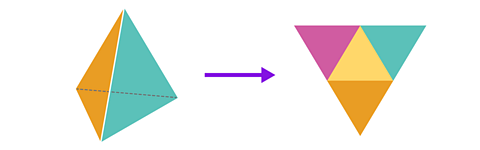
tetrahedron (triangular pyramid) and next to a net of a tetrahedron with 4 triangles. 3 triangles are connected in a row, and the fourth triangle under the central triangle forming a pattern that can be folded into pyramid shape.

Can you see that a tetrahedron has 4 triangle faces?

Now let’s look at the net of another shape.

Here is the net of a triangular prism.

A triangular prism next to its unfolded net. The triangular prism has 2 triangular faces and 3rectangular faces. The net has 2 triangles and 3 rectangles to show the 3 rectangular sides of the prism.

Can you see that a triangular prism has 5 faces. It has 2 triangle faces and 3 rectangle faces.

When you have the net of a 3D shape, look carefully at the shape of each face and the number of faces to work out which 3D shape it is.

Back to top

Example

Another name for a tetrahedron is a triangular pyramid.

Other pyramids are named after the shape of the polygon at the base.

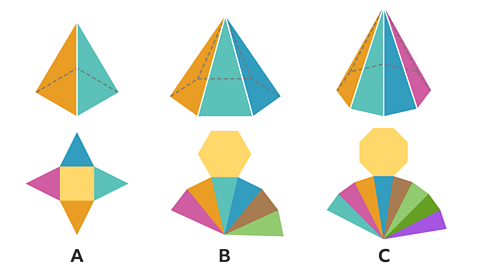
Top row, a square pyramid, with one square and 4 triangles. A hexagonal pyramid, with 1 hexagon and 6 triangles and an octagonal pyramid, with 1 octagon and 8 triangles. Bottom row has 3 net shapes showing A, a net of a square pyramid, with 1 square and 4 triangles. The square is in the centre, with a triangle attached to each of its four edges, making a shape that can be folded into a pyramid with a square base. B, a hexagonal pyramid, with 1 hexagon and 6 triangles. The hexagon is in the centre, with a triangle attached to each of its six edges, making a shape that can be folded into a pyramid with a hexagonal base. C, an octagonal pyramid, with 1 octagon and 8 triangles. The octagon is in the centre, with a triangle on each of its 8 edges, making a shape that can be folded into a pyramid with an octagonal base.

What are the names for these pyramids?

Back to top

Use your times tables and more maths skills to defeat monsters and reclaim the Kingdom of Mathematica

Play our fun maths game Guardians: Defenders of Mathematica
Back to top

More on 2D shapes

Find out more by working through a topic