What are remainders?

Sometimes it is not possible to divide one number by another exactly.
Anything left over that cannot be divided exactly is called the remainder.
When you are solving problems and there is a remainder, you need to know what to do with it.
There are different ways of representing the remainder.
They can be represented as just a remainder, a fraction or a decimal.

Activity: Working out division with remainders
Complete this interactive activity to understand how to work out the answer to division problems with remainders. Then put your knowledge to the test.
Representing the remainder
Let's look at a question.
'If 232 bananas need to be packed into bags of 5, how many bags would be needed?'
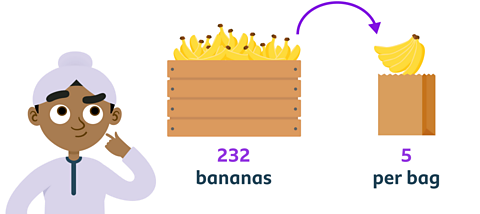
The division calculation you need to complete is:
232 ÷ 5 =
If 232 bananas needed to be packed into bags of 5, you would need 46 bags and 2 single bananas would be left over.
You could show this remainder in some different ways.
The simplest way of working with a remainder when dividing numbers is just to leave the remainder.
You write a 'r' next to the number to show that it is the remainder, like this:

To represent the remainder as a fraction, all you need to do is write the remainder as the numerator, and the divisor as the denominator.
2 is the remainder and 5 is the divisor.
The fraction would be \(\frac {2} {5}\).

Another way of representing the remainder is to use a decimal point and continue the division into the tenths and hundredths columns.
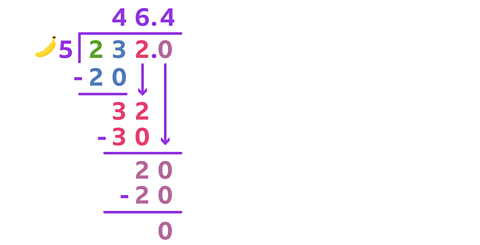
When solving problems with division, you have to decide which of these ways of representing the remainder is the best.
Which way do you think would be best for the question about the bananas?
Example 1
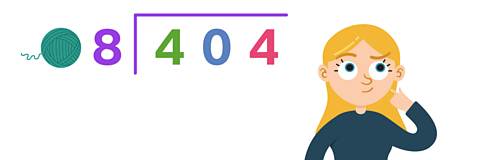
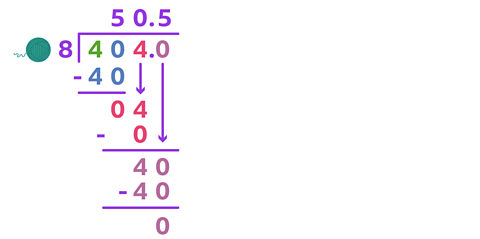
Lucy has a length of wool measuring 404 centimetres.
She needs to cut it into 8 equal pieces.
How long will each length of wool be?
✓ Each length of wool would be 50.5 cm long.
Example 2

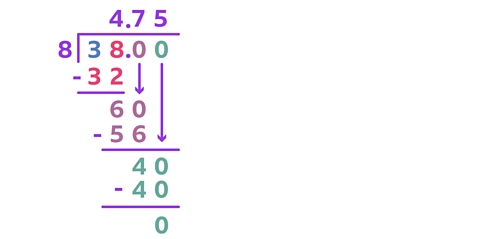
If you worked out 38 ÷ 8, how would you represent the remainder in both decimals and with a fraction?
✓ The answer is 4.75, or 4 \(\frac {3} {4}\).
To work out the fraction remainder, you write the remainder at the numerator and the divisor as the denominator.
In this calculation, the fraction remainder is \(\frac {6} {8}\). This can be simplified to \(\frac {3} {4}\).
The remainder represented by decimals is .75
Example 3

Calculate 800 ÷ 30. What happens?
✓ Once you have divided all of the whole numbers, you are left with 20 tenths.
Keep working through the division to see what happens.
How many groups of 30 tenths can you make if you have 200 tenths?
You can make 6 groups of 30 tenths, which is 180, with 20 tenths left over.
Exchange the 20 tenths for 20 hundredths.
How many groups of 30 hundredths can you make if you have 200 hundredths?
You can make 6 groups of 30 hundredths, which is 180, with 20 hundredth left over…
Can you see what is happening here? Each time there is 20 left over, and this will go on and on and on!

This is called a repeating decimal remainder or a recurring decimal. It will repeat forever!
When this happens, it is better to leave the remainder as a fraction. Or - if you know how to round numbers, you could round the hundredth digit up or down.
Here, the remainder will be \(\frac {20} {30}\), or \(\frac {2} {3}\), so the answer is 26 \(\frac {2} {3}\)
Or if you round to the nearest hundredth, the answer is 26.67.
Play our fun maths game Guardians: Defenders of Mathematica. gamePlay our fun maths game Guardians: Defenders of Mathematica
Use your times tables and more maths skills to defeat monsters and reclaim the Kingdom of Mathematica

More on Multiplying and dividing
Find out more by working through a topic
- count2 of 4

- count3 of 4
