Multiply a mixed number by an integer

You can multiply a mixed number by an integer using two different methods.
You can convert the mixed number into an improper fraction.
An improper fraction has a numerator greater than its denominator.
The other way is to use partitioning, which means multiplying the individual parts of the fraction then combining them.

Activity: Multiply mixed numbers by an integer
Complete this interactive activity to learn more about how to multiply mixed numbers by integer and then put your knowledge to the test with a quiz.
Converting to a top heavy fraction
A mixed number is a number where there is a whole number and a fraction, for example \( 2 \frac{2}{3} \).
An integer is any whole number. This can be a positive number, a negative number, or 0.
Let’s have a look at the first method for multiplying a mixed number by an integer. Here is a calculation:

You first need to change the mixed number into a top heavy fraction.
In \( 3 \frac{1}{5} \) there are 16 fifths altogether, so you can write this as the top heavy fraction \( \frac{16}{5} \).

You can then multiply this top heavy fraction by 4.
You have 4 lots of 16 fifths, which is 64 fifths, or \( \frac{64}{5} \).

Remember, when multiplying fractions you multiply the numerator (top number) by the integer (whole number). The denominator (bottom number) stays the same.
\( \frac{64}{5} \) is a top heavy fraction. You can now convert this back into a mixed number.
From the 64 fifths, you can make 12 wholes and \( \frac{4}{5} \).

\( \frac{64}{5} \) as a mixed number is \( 12 \frac{4}{5} \).
Therefore:
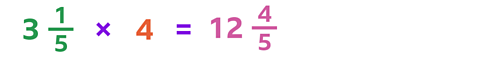
Using partitioning
Another way to multiply a mixed number by an integer is to use partitioning.
Let’s look at the same question again, but this time let's use partitioning to solve it.

You can partition a mixed number into the whole number and the fraction.
So '\( 3 \frac{1}{5} \)' becomes a ‘3’ and '\( \frac{1}{5} \)’.
Once you have partitioned the mixed number, you can multiply both parts by the integer.
Start by multiplying the whole numbers together:

Now you have to multiply the fraction by the integer.
So here you will have 4 lots of one fifth, which is four fifths, or \( \frac{4}{5} \).

Now all you have to do is work out how much you have altogether.
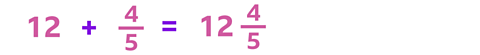
It doesn't matter which method you choose, you can see that the answer is the same.
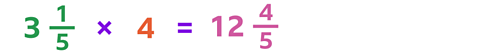
Example 1
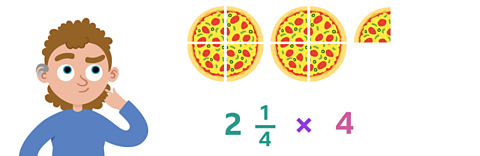
Solve this calculation:
\( 2 \frac{1}{4} \) × 4 = ?
✓ First you could convert the \(2 \frac{1}{4} \) into a top heavy fraction. This gives you \( \frac{9}{4} \).
\(2 \frac{1}{4} \) = \( \frac{9}{4} \)
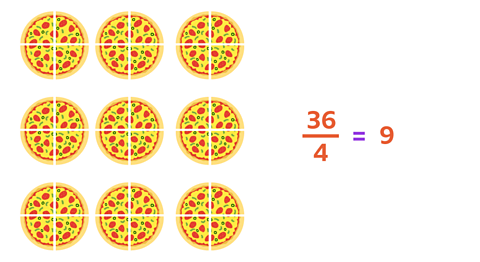
Then you can multiply this by 4, which is \( \frac{36}{4} \).
\( \frac{9}{4} \) × 4 = \( \frac{36}{4} \)
\( \frac{36}{4} \) is the same as 9.
\( \frac{36}{4} \) = 9
Example 2
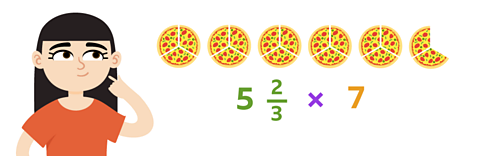
Solve this calculation:
\(5 \frac{2}{3} \) × 7 = ?
✓ Using partitioning you can separate the whole number from the fraction and multiply them both by 7.
5 × 7 = 35
\( \frac{2}{3} \) × 7 = \( 4 \frac{2}{3} \)
Now work out how much you have altogether.
35 + \( 4 \frac{2}{3} \) = \( 39 \frac{2}{3} \)
Example 3

Each delivery bag contains 4 whole pizzas and \( \frac{2}{3} \) of a pizza.
If 8 bags of pizza are delivered, how much pizza will there be altogether?
✓ The calculation you need to do is:
\(4 \frac{2}{3} \) × 8 = ?
This becomes:
32 + \( \frac{16}{3} \) = ?
The \( \frac{16}{3} \) can also be written as \(5 \frac{1}{3} \) which gives you:
32 + \(5 \frac{1}{3} \) = ?
Then by adding the whole numbers you get:
32 + \(5 \frac{1}{3} \) = \(37 \frac{1}{3} \)
Play our fun maths game Guardians: Defenders of Mathematica. gamePlay our fun maths game Guardians: Defenders of Mathematica
Use your times tables and more maths skills to defeat monsters and reclaim the Kingdom of Mathematica

More on Fractions
Find out more by working through a topic
- count3 of 4

- count4 of 4

- count1 of 4
