Introducing simultaneous equations
We have looked at how to solve equations with one unknown value, but what happens when there are two unknown values?
An equation with two unknown values will have infinitely many solutions.
Example
\(x + y = 10\) has infinitely many values for \(x\) and \(y\) for which this is true, such as:
\(x=1\), \(y=9\)
or \(x=10\), \(y=0\)
or \(x=100\), \(y=-90\), etc.
But you can use two equations together, if they have the same two unknowns, to make one equation that has only one solution.
\(x\) and \(y\) values can be found which will solve both of the original equations at the same time or simultaneously.
A pair of equations like this are called simultaneous equations - because you are trying to solve them both with the same values for \(x\) and \(y\).
Solving simultaneous equations by substitution
Substitution method
Example
Solve the simultaneous equations:
\(y = 2x\)
\(x + y = 6\)
One way to solve them is by using the substitution method.
Begin by labelling the equations (1) and (2):
\(y = 2x\) (1)
\(x + y = 6\) (2)
Equation (1) tells you that \(y = 2x\), so substitute this value of \(y\) into the second equation, ie replace \({y}\) with \({2x}\).
\(x + 2x = 6\)
\(3x = 6\)
\(x = 2\)
This gives you the value of \(x\), but what is the value of \(y\)?
Equation (1) tells you that \(y = 2x\), so \(y\) must be \(4\).
You can check your answer in the other equation - in this case, (2).
\(2 + 4 = 6\)
This is right, so the values are correct.
The solution of the equations is therefore:
\(x=2\), \(y=4\)
Question
Use the substitution method to solve the following simultaneous equations:
\(y = x + 2\)
\(2x + y = 11\)
Answer
First label the equations.
\(y = x + 2\) (1)
\(2x + y = 11\) (2)
Substitute the value of \(y\) from equation (1) into equation (2):
\(2x + (x + 2) = 11\)
\(3x + 2 = 11\)
\(3x = 9\)
\(x = 3\)
To find \(y\) use this \(x\) value in equation (1): \(y = x + 2 = 3 + 2 = 5\)
Check in equation (2): \((2 \times 3) + 5 = 11\) (which is correct)
So the solution is:
\(x = 3\), \(y = 5\)
Solving simultaneous equations algebraically
Algebraic method
You can solve simultaneous equations by adding or subtracting the two equations in order to end up with an equation with only one unknown value.
This is known as the algebraic method.
Example
Solve the simultaneous equations:
\(2x + y = 9\) (1)
\(3x - y = 1\) (2)
Add the two equations together and you will find that the \(y\) disappears:
\(3x + 2x + y - y = 9 + 1\)
This can be simplified to:
\(5x = 10\)
\(x = 2\)
Substituting this value of \(x\) in (1) gives:
\(4 + y = 9\)
\(y = 5\)
Check in (2):
\(6 - 5 = 1\) (which is correct)
So the solution is:
\(x=2\), \(y=5\)
Question
Solve the simultaneous equations:
\(3x + 2y = 8\)
\(3x - y = 5\)
Answer
Firstly use labels for the equations:
\(3x + 2y = 8\) (1)
\(3x - y = 5\) (2)
To make the \(3x\)s disappear we can subtract equation (2) from equation (1):
\(3x - 3x + 2y - (-y) = 8 - 5\)
This simplifies to:
\(3y = 3\)
\(y = 1\)
Substitute in (1):
\(3x + 2 = 8\)
\(3x = 6\)
\(x = 2\)
Check in (2):
\(6 - 1 = 5\) (which is correct)
So the solution is:
\(x = 2\), \(y = 1\)
Sometimes equations need to be altered, by multiplying throughout, before being able to eliminate one of the variables (letters).
Example
Solve the simultaneous equations:
\({2x} + {3y} = {9}\) (1)
\({3x} + {y} = {10}\) (2)
Neither the \(x\) nor the \(y\) will be eliminated by adding or subtracting these equations as they stand.
By multiplying the second equation by \({3}\) throughout, both equations will then include \({3y}\), which will allow us to continue with the solution.
(2)\(\times~{3}\) gives \({9x} + {3y} = {30}\) (3)
Don’t forget to multiply the right hand side by \(3\) as well.
Now, looking at equations (1) and (3), as they both include ‘\(+{3}{y}\)’, we will subtract one equation from the other.
Subtract equation (1) from equation (3) and you’ll find that the \(y\) disappears:
\((9x+3y)-(2x+3y)=30-9\)
This can be simplified to:
\({7x} = {21}\)
\({x} = {3}\)
Substituting this value of \(x\) in (1) gives:
\({2}\times{3}+{3y}={9}\)
\({6}+{3y}={9}\)
\({3y}={3}\)
\({y}={1}\)
Check in (2):
\({9} + {1} = {10}\) (which is correct)
So the solution is:
\({x}={3}\), \({y}={1}\)
Question
Solve the simultaneous equations:
\({5x} + {3y} = {21} \)
\({x} - {y} = {1}\)
Answer
Firstly use labels for the equations:
\({5x} + {3y} = {21}\) (1)
\({x} - {y} = {1}\) (2)
To make the \(y\)s disappear we need to multiply equation (2) by \({3}\) before adding to equation (1):
(2) \(\times~{3}\) gives \({3x} - {3y} = {3}\) (3)
By adding equation (1) and equation (3) and you will find that the \({y}\) disappears:
\(({5x} + {3y}) + ({3x} - {3y}) = {21} + {3}\)
This can be simplified to:
\({8x} = {24}\)
\({x} = {3}\)
Substitute in (1):
\({5}\times{3}+{3y}={21}\)
\({15}+{3y}={21}\)
\({3y}={6}\)
\({y}={2}\)
Check in (2):
\({3} - {2} = {1}\) (which is correct)
So the solution is:
\({x}={3}\), \({y}={2}\)
Solving simultaneous equations graphically
As well as solving simultaneous equations algebraically, you can solve them by rearranging them into the form of \(y = mx+c\) so that you can plot them as straight line graphs.
When you have plotted the graphs, you can work out the values of \(x\) and \(y\) that solve the equations.
How do you solve simultaneous equations using graphs?
How to solve simultaneous equations using graphs.
How much is each ticket?
Draw a bar to represent one adult and two children’s tickets.
Let’s call the adult ticket 𝑦 and the child ticket 𝑥.
Another bar represents the total of £7.
Do the same for the second set of tickets.
And simplify the diagram by writing 2𝑥.
And on the other, 5𝑥.
You can see that 𝑦 + 2 = 7.
Which means 𝑦 = 7 – 2𝑥.
You can also rewrite the second equation, 𝑦 = 13 – 5𝑥.
Now, draw their graphs.
First, draw a table of values.
Start with 𝑥 = 0 and substitute this into our equation.
When 𝑥 = 0, 𝑦 = 7.
Next, substitute 𝑥 = 1.
𝑦 = 5.
Substitute up until 𝑥 = 4.
We need to do the same again for the equation, 𝑦 = 13 – 5𝑥, with a new table of values and substitute 𝑥 = 0.
𝑥 = 1.
𝑥 = 2.
𝑥 = 3.
And, finally, 𝑥 = 4.
You now have five pairs of co-ordinates for both line graphs and you need to plot them both on the same axes.
Draw the 𝑥 and 𝑦 axes. Make sure the 𝑥-axis includes the values 0 to 4, and the 𝑦-axis the values –7 to 13.
Plot the co-ordinates on the axes. Remember, the 𝑥 co-ordinate is always first.
We’ve plotted the points from the first table. Join these points with a straight line.
𝑦 = 7 – 2𝑥.
Now, plot the co-ordinates from our second table. Join these points with a straight line.
𝑦 = 13 – 5𝑥.
Both lines cross each other at one co-ordinate: when 𝑥 = 2 and when 𝑦 = 3.
This means our 𝑥 value is 2 and our 𝑦 value is 3.
So, the adult ticket, 𝑦, is £3.
And the child ticket, 𝑥, is £2.
Simultaneous equations

Image caption, Click here to see a step by step slideshow.

Image caption, You can solve problems like this using simultaneous equations.

Image caption, STEP 1 - Convert the problem into algebraic notation. In this example the adults are represented by y, and the children are represented by x. So y + 2x = 7 and y + 5x = 13.

Image caption, STEP 2 - The equations can be rearranged so that they both start with y =. So y = 7 – 2x and y = 13 – 5x. These will be our pair of simultaneous equations.

Image caption, STEP 3 - Starting with x = 0, work out the y values for each equation. For example, put x = 0 into the equation y = 7 – 2x. So y = 7 – (2 x 0). Making y = 7. Continue to do this with all of the x values up to 4.

Image caption, STEP 4 - Repeat this process for y = 13 – 5x. For example, put x = 4 into the equation: y = 13 – (5 x 4). Making y = -7. Do this for the rest of the x values 0, 1, 2, 3 and 4.

Image caption, STEP 5 - Draw a graph with x and y axes using the values you have found.
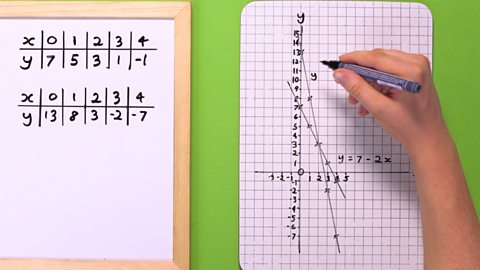
Image caption, STEP 6 - Plot the x and y values you have calculated as coordinates on the graph. Draw a line for the first set of values, and then draw a line for the second set.

Image caption, STEP 8 - Find the point where the lines intersect. The point of intersection is (2, 3). So x = 2 and y = 3.
1 of 9
Example
Use the graphical method to solve the simultaneous equations:
\(y = 2x\)
\(2x + y = 8\)
Start by rearranging the two equations to get them in the form:
\(y = mx + c\)
In this case you only need to rearrange the second equation. The two equations are now:
\(y = 2x\)
\(y = -2x + 8\)
Plotting the graph
We now have two equations of straight line graphs, which we can plot.
When we do this we can look at where the two lines cross (the point of intersection).
The values of \(x\) and \(y\) at this point are the solutions of the simultaneous equations.
The solution of this pair of simultaneous equations is:
\(x = 2\), \(y = 4\)
Test yourself
Question 1
Use the substitution method to solve these simultaneous equations: \({y}={3}{x}\), \({2}{x}+{y}={5}\)
Answer
You need to substitute \({y}={3}{x}\) in the second equation to get \({5}{x}={5}\), and get \({x}={1}\) after solving it.
Substitute \({x}={1}\) in the first equation which gives \({y}={3}\).
Question 2
Use the substitution method to solve these simultaneous equations: \({y}={-2}{x}\), \({3}{x}-{2}{y}={-7}\).
Answer
You need to substitute \({y}={-2}{x}\) in the second equation to get \({3}{x}+{4}{x}={-7}\) and go on from there.
The correct answer is: \({x}={-1},~{y}={2}\)
Question 3
Use the algebraic method to solve these simultaneous equations: \({2}{x}+{y}={8}\), \({5}{x}-{y}={13}\)
Answer
You need to add the two equations to get \({7}{x}={21}\) and go on from there.
The correct answer is: \({x}={3},~{y}={2}\)
Question 4
Use the algebraic method to solve these simultaneous equations: \({x}+{y}={1}\), \({x}+{4}{y}={-23}\).
Answer
By subtracting the first equation from the second, you'll get \({3}{y}={-24}\) which gives \({y}={-8}\).
Substituting the value of \({y}\) and calculating you get \({x}={9}\).
Question 5
Use the algebraic method to solve these simultaneous equations: \({2}{x}+{y}={7}\), \({10}{x}+{y}={11}\).
Answer
By subtracting the first equation from the second, you'll get \({8}{x}={4}\), which gives \({x}={0.5}\).
Then you'll need to calculate \({y}\).
The correct answer is: \({x}={0.5},~{y}={6}\)
Question 6
Use the algebraic method to solve these simultaneous equations: \({2}{p}-{7}{q}={13}\), \({2}{p}-{3}{q}={1}\).
Answer
The correct answer is: \({p}={-4},~{q}={-3}\).
Question 7
Use the algebraic method to solve these simultaneous equations: \({4}{w}+{3}{z}={9}\), \({8}{w}+{5}{z}={13}\).
Answer
You need to double the first equation before subtracting and then you should get \({z}={5}\).
\({w}\) = \({-1.5}\).
Question 8
Use the graphical method to solve these simultaneous equations: \({y}={3}{x}-{3}\), \({y}={-x}+{5}\).
Answer
You need to plot two straight lines using the equations, then see where they cross.
So, the correct answer is: \({x}={2},~{y}={3}\)
Question 9
Use the graphical method to solve these simultaneous equations: \({y}+{2}{x}={6}\), \({y}={x}+{3}\)
Answer
The correct answer is: \({x}={1},~{y}={4}\).
You need to rewrite the first equation as \({y}={-2}{x}+{6}\).
That should help you plot the lines and find the point of intersection.
Question 10
Use the graphical method to solve these simultaneous equations: \({2}{x}+{y}={8}\), \({3}{x}+{y}={9}\).
Answer
You need to draw the graphs of the two equations and see where they cross.
So, the correct answer is: \({(1,6)}\).
More on Simultaneous equations
Find out more by working through a topic