Module 2 (M2) - Geometry and measures - Compound measures

Part ofMathsM2: Geometry and measures

Compound Measures

Compound measures involve two or more different units. Examples of compound measures and their units include density (g/cm3), speed (km/h), heart rate (beats per minute), miles per gallon (mpg)

Remember

Units for measuring such as metres, kilograms and litres are covered in Metric Units and are examples of single units. Compound units at M1 covers speed, heart rate and fuel economy.

Back to top

Density

Calculating density given mass and volume

Density is a measure of how much mass an object has per unit volume. Density is a compound measure because mass and volume are measured in different units.

Density is calculated by dividing the mass of an object by the volume.

\(\text Density = \frac{Mass}{Volume}\) or \(D = \frac{M}{V}\)

This triangle can be helpful for remembering the formula.

DMV triangle
Back to top

Example

Aluminium is a very low-density metal and is used to build all sorts of vehicles.

Calculate the density of aluminium if 20 cm3 has a mass of 54 g.

  • Mass = 54 g
  • Volume = 20 cm³

Using \(Density = \frac{Mass}{Volume}\)

\(Density = \frac{54}{20} = 2.7g/cm^3\)

DMV Triangle
This triangle can be helpful for remembering the formula.
Back to top

Question

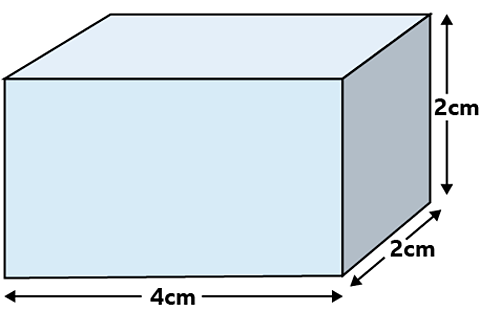
A block has a mass of 6.4 g and dimensions 2 cm by 4 cm by 2 cm.

Calculate

  1. the volume of the block.
  2. the density of the block.

Back to top

Calculating mass given density and volume

If the density and volume are known, the formula can be rearranged to calculate mass by multiplying both sides by volume.

\(\large {\mathbf{\color{orange}{Volume} \color{black}\times Density = \frac{Mass}{\cancel{Volume}} \times \color{orange}\cancel{Volume}}}\)

\(\textbf{Mass = Volume} \times\textbf{Density}\)

\(M = V \times D\)

DMV triangle
Back to top

Example

A ring is made from 2.4 cm3 of gold. Calculate the mass of the ring given that the density of gold is 19.3 g/cm3.

  • Volume = 2.4 cm³
  • Density = 19.3 g/cm³

Using
\(Mass = Volume \times Density\)

Mass = 2.4 x 19.3 = 46.32 g

Back to top

Question

Maisie makes jewellery and has a 1000 cm3 block of silver and the same amount of nickel.
What is the difference between the masses of the two blocks?

Density

  • Silver - 10.5 g/cm³
  • Nickel - 8.9 g/cm³

Back to top

Calculating volume given density and mass

If the density and mass are known the formula can be rearranged to calculate the volume.

\(Volume = \frac{Mass}{Density}\)

\(V = \frac{M}{D}\)

DMV triangle

Example

Water has a density of 1 g/cm3. Given that the mass of water in a bottle is 0.5 kg, calculate the volume of water in the bottle, giving your answer in litres.

  • Density = 1 g/cm3
  • Mass = 0.5 kg = 500 g

Take care to use the same units!

\(Volume = \frac{Mass}{Density}\)

\(Volume = \frac{500}{1}= 500\)

Volume = 500 cm³ The answer should be given in litres.

= 500 ml 1 cm3 = 1 ml

= 0.5 l

Back to top

Question

The density of iron is 7870 kg/m³.

Calculate the volume of an iron sculpture which has a mass of 550 kg.

Back to top

Test yourself

Back to top

More on M2: Geometry and measures

Find out more by working through a topic