Definitions of perpendicular, bisector and locus
If two lines are drawn at right angles to each other, they are said to be perpendicular.
A line drawn to cut another line or angle in half is a bisector.
The path of a point that moves according to a certain rule is a locus.
The plural of locus is loci.
Perpendicular bisector of a line segment
Practise these constructions until you can do them without looking at the instructions.
Follow the instructions and draw this perpendicular bisector of a line segment construction.
Perpendicular bisector construction of a line segment

Image caption, Begin by drawing a straight horizontal line.
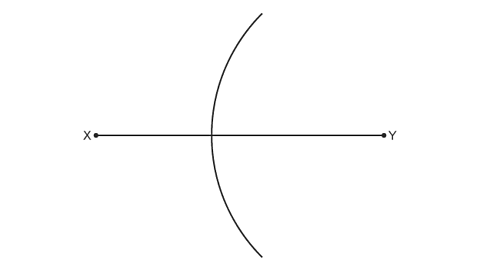
Image caption, Placing your compass at one end of the line, draw an arc - making sure it is over half way across the line.
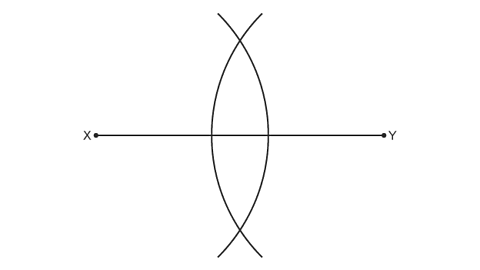
Image caption, Without changing the distance between the pencil and compass point, place your compass at the other end of the line and draw another arc - crossing the first arc in two places.
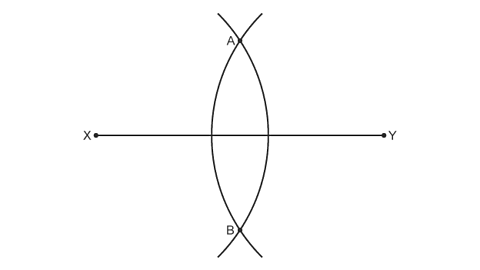
Image caption, The points where the arcs cross (A and B) are exactly the same distance from X and Y.
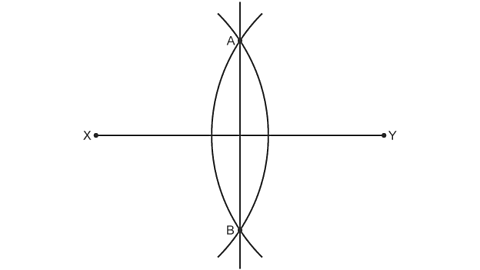
Image caption, Use your ruler to draw a line connecting the points A and B.
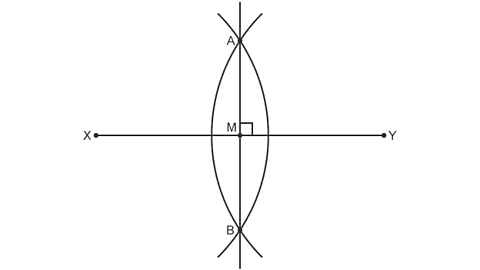
Image caption, Point M is exactly halfway between X and Y. When drawn correctly, these lines will always be at right angles.
1 of 6
Draw a perpendicular from a point to a line
Follow the instructions and draw the perpendicular from a point to a line construction.
Perpendicular from a point on a line construction

Image caption, Begin with a straight horizontal line and mark point P over the line.
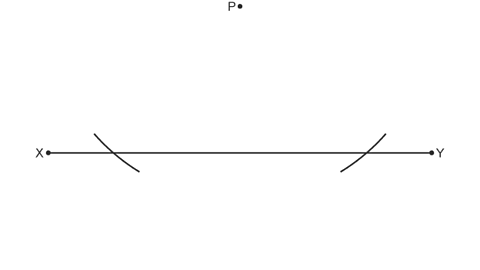
Image caption, Placing your compass on the point, mark the line in two places.
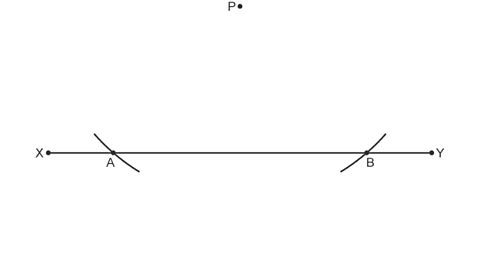
Image caption, Label the points A and B.
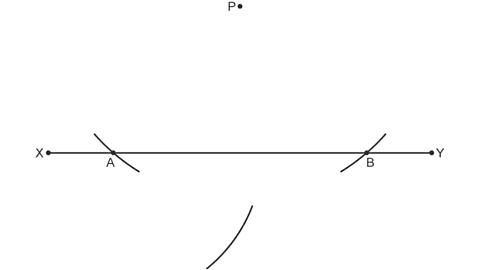
Image caption, Placing your compass on point A, draw an arc - making sure it is over half way across AB, but below the line.
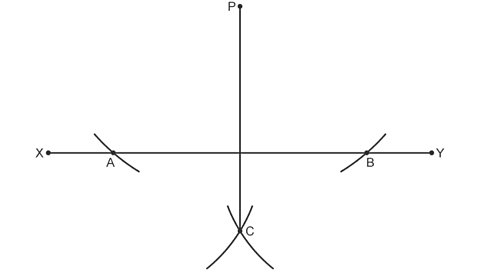
Image caption, Without changing the distance between your compass point and pencil, place the compass on point B and do the same - making sure the two arcs cross. Mark this point C. Finally, draw a line connecting points C to the original point P. Line PC is perpendicular to XY.
1 of 5
Draw a perpendicular through a point on a line
Follow the instructions and draw the perpendicular through a point on a line construction.
Perpendicular from a point on a line construction
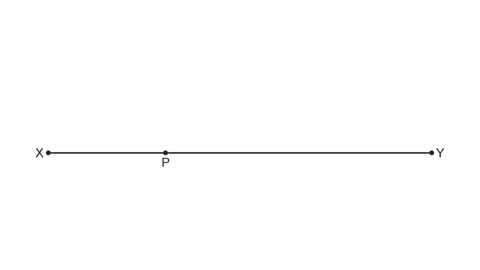
Image caption, Draw a straight horizontal line and mark a point, P, anywhere on the line.
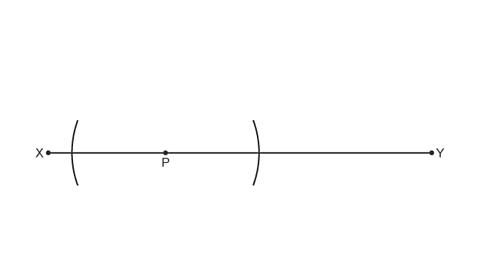
Image caption, Placing your compass point on P, draw arcs on both sides of P.
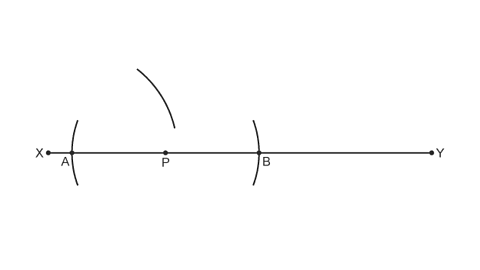
Image caption, Placing your compass on point A, draw an arc - making sure it is over half way across AB, but above the line.
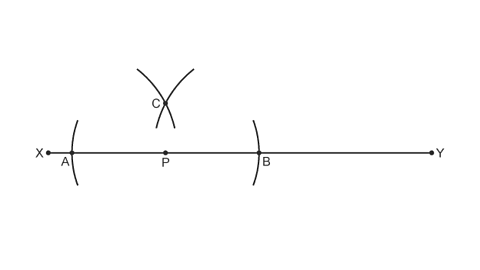
Image caption, Without changing the distance between your compass point and pencil, place the compass on point B and do the same - making sure the two arcs cross.
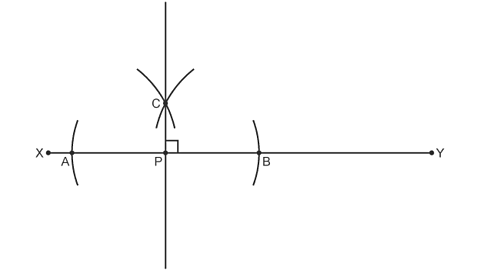
Image caption, Finally, draw a line connecting points C to the original point P. Line CP is perpendicular to XY.
1 of 5
Follow the instructions and draw this angle bisector construction.
Angle bisector construction
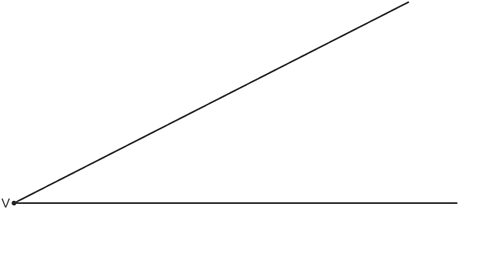
Image caption, Begin by drawing two lines, meeting at a point. Mark this point V.
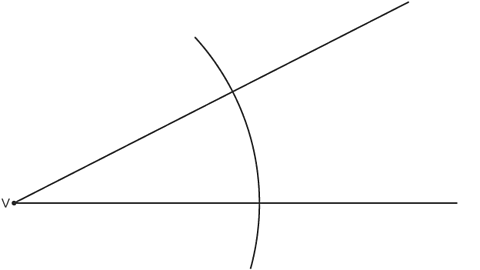
Image caption, Place your compass on the point where the lines meet, draw an arc that crosses both lines.
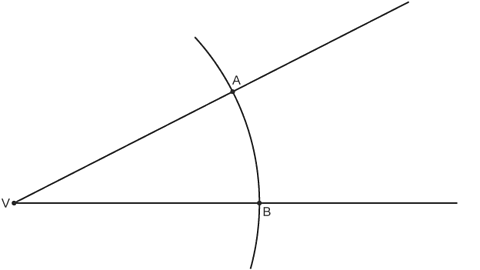
Image caption, Label the points A and B.
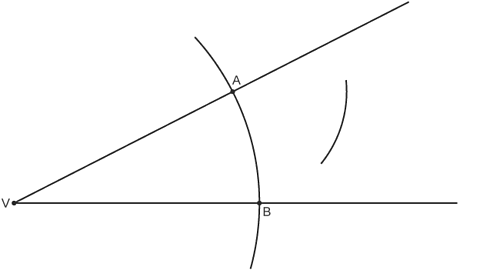
Image caption, Place your compass on the point A, draw an arc towards the middle.
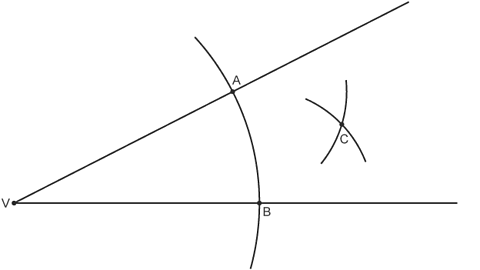
Image caption, Without changing the distance between your compass point and your pencil, place the compass on point B and draw an arc towards the middle - making sure that the two arcs cross. Mark this point C.
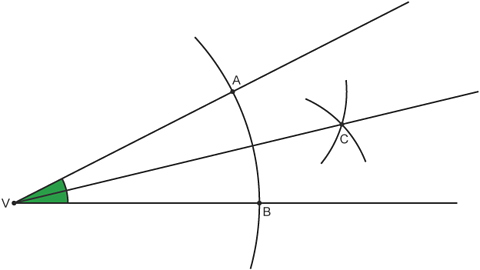
Image caption, Finally, using a ruler connect point C to point V. Line VC bisects the angle AVC.
1 of 6
Loci
Locus
A cow is tethered to a post with a rope of length \({4~m}\).
It walks around the post with the rope pulled tight.
The cow's path is a circle of radius \({4~m}\).
The cow's path is known as the locus.
The plural of locus is loci.
Three-figure bearings
Suppose you were in the middle of nowhere, and there were no signs or landmarks to help you find your way.
Would you know how to find your way home?
Someone might tell you via phone or radio to 'walk to your left', or 'turn through \({60}^\circ\) and then start walking', but how would they know which way you were pointing in the first place?
One way of describing direction from a point is to use three-figure bearings.
Compass
A compass always points north. Bearings are measured from the north line, always in a clockwise direction.
So when someone tells you to walk on a bearing of \({120}^\circ\), you should face north, turn clockwise through \({120}^\circ\) and start walking.
Key fact
Bearings are always described using three figures.
So for less than 100° put an appropriate number of 0s in front, eg 020°, 037°, 002°, 007°.
Example
An aeroplane takes off from Belfast International airport, as shown in the diagram below.
The angle between the north line and the flight path of the aeroplane is \({30}^\circ\).
So we can say that the aeroplane is flying on a bearing of \({030}^\circ\) from Belfast International airport.
Finding a way to the gig…
Follow one teenager's adventure as he gets lost and attempts to use bearings and loci to get him to the gig on time.
(MUSIC)
BEN:
No. Oh no. No!
(MUSIC)
Mae! Mae! Can you hear me? Are they on yet!?
I don’t know how to get there. That’s the point.
All that money for a festival ticket and I am not missing them.
They’re my favourite band.
But you told me to go this way.
Is that them playing?
I can’t use maps, I’ve got no data signal.
Hang on, I’ve got a compass app.
Did you say 81 degrees?
I heard 81 but that could be 81, 181, 281?
I don’t want to get it wrong!
Look, the proper way is to always use three digits — 081 degrees.
OK, look I’ll take it from here.
Right, I know how to work out a bearing.
You need to give all the instructions clockwise from north.
First of all, let’s find north.
(MUSIC)
So start with north. Great, that’s north.
Now we’ve got to turn clockwise.
Clockwise is always turning to the right.
The circle is split up into 360 degrees.
Let’s see if we can find 081 degrees.
There we go.
So from north to 081. Way to go!
(MUSIC)
Oh no, I hate dogs!
(DOG GROWLS)
They look quite vicious.
(DOG GROWLS)
Well, if they weren’t on a lead…
I know all about this. It’s loci — that’s what it is.
Because of the length of the rope, the dogs can only move a set distance from the post and from the fence.
The path they follow is the locus.
So if I imagine this as a plan with the post and a fence and me here…
Dog one has a lead of, say, four metres — he can run round and round the post.
So the path that defines his locus is a circle.
On the other side, the lead of Dog two can slide up and down this section of fence.
So the locus of the line between the two fence posts would in theory be this.
But in the real world, the fence will keep the dog in this area.
So if they both rush me at once…
There’s still a small corridor for me to get through.
Slowly does it…
(DOG GROWLS)
Careful there…
(DOG GROWLS)
Stay where you are…
(DOG GROWLS)
Phew!
Right then, let’s get to that gig.
Wahey!
(ROCK MUSIC)
Test section
Question 1
What are perpendicular lines?
Answer
Perpendicular lines are two lines drawn at right angles to each other.
Question 2
What is a bisector?
Answer
A bisector is a line drawn to cut another line or angle in half.
Question 3
What is 'the path of a point that moves according to a certain rule'?
Answer
The path of a point that moves according to a certain rule is a locus.
Question 4
Which mathematical apparatus, in addition to a pencil and ruler, is needed to find the midpoint of a line segment?
Answer
You need to use a compass as well as a pencil and ruler to find the midpoint of a line segment.
Question 5
How many arcs do you need to draw when constructing a perpendicular to a line through a point on the line or above it?
Answer
You need to draw \({4}\) arcs when constructing a perpendicular to a line through a point on the line or above it.
Question 6
What is the minimum number of arcs needed to construct an angle bisector correctly?
Answer
You need to draw a minimum of \({3}\) arcs to construct an angle bisector correctly.
Question 7
What is the locus of a point that's \({6}~{cm}\) from a fixed point?
Answer
The locus of a point that's \({6}~{cm}\) from a fixed point is a circle of radius \({6}~{cm}\).
Question 8
What is the locus of a point that's further than \({2}~{cm}\) from a fixed point and less than \({6}~{cm}\) from the same point?
Answer
The locus of a point that's further than \({2}~{cm}\) from a fixed point and less than \({6}~{cm}\) from the same point is shaped like a circle with a hole in the middle.
Question 9
What does this construction represent?
Answer
The correct answer is: a perpendicular through a point, P, on the line XY
The first arcs are drawn here from P, and then the perpendicular line has been drawn to pass through the point P.
Question 10
What does this construction represent?
Answer
The correct answer is: a perpendicular from a point, P, onto the line XY.
More on Constructions
Find out more by working through a topic
- count2 of 4

- count4 of 4
