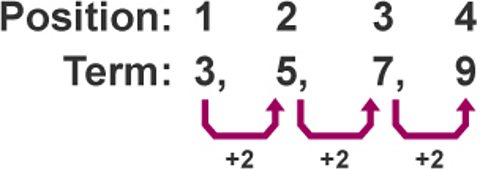What is a ratio?
Ratios are used to show how things are shared. For example, the necklace in the image below has a pattern of two red beads for every three yellow beads.
The ratio of red beads to yellow beads is \(2:3\).
Ratios can have more than two numbers for example, \(3:4:2\).
Simplifying ratios
Ratios can be fully simplified just like fractions.
To simplifyA fraction is simplified when there are no more common factors shared by the numerator and denominator. For example, the fraction 8/10 simplifies to 4/5 by dividing the numerator and denominator by the common factor of 2. a ratio, divide all of the numbers in the ratio by the same number until they cannot be divided any more.
Example
Simplify \(6:12\).
Solution
Divide both numbers by 2:
\(6:12=3:6\)
Divide both numbers by 3:
\(3:6=1:2\)
A quick way of doing this in just one step is to divide by the highest common factor of all the numbers in the ratio. In this example, the highest common factor of 6 and 12 is 6. Dividing each number by the HCF:
\(3:6=1:2\)
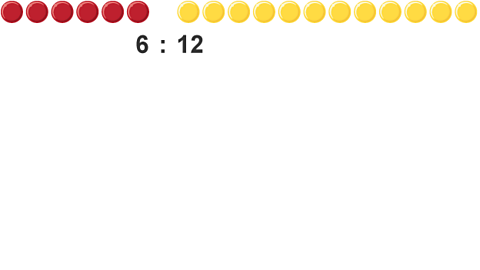
Image caption, A ratio of 6:12 with 6 red coloured counters and 12 yellow coloured counters spread out horizontally.
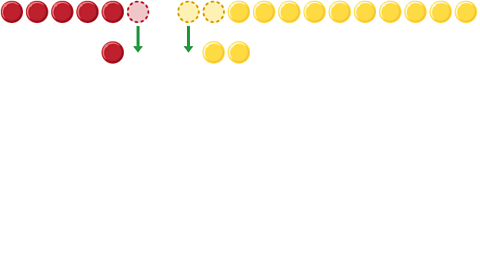
Image caption, One red counter and two yellow counters move from the group and line up next to each other under the group
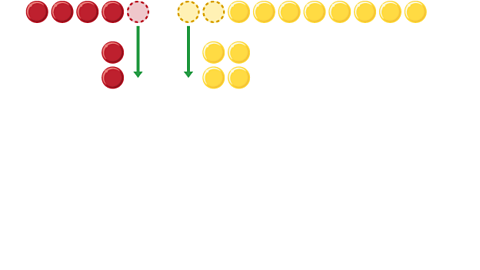
Image caption, One red counter and two yellow counters move with each step
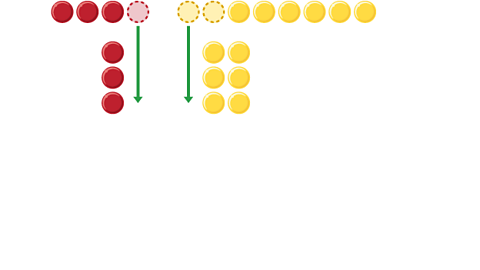
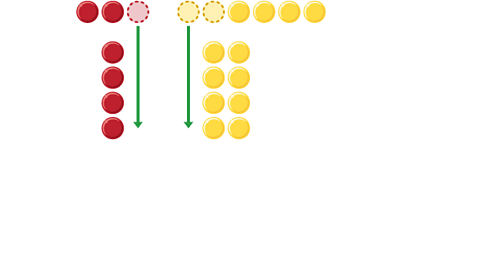
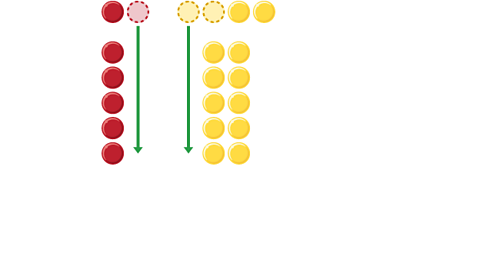
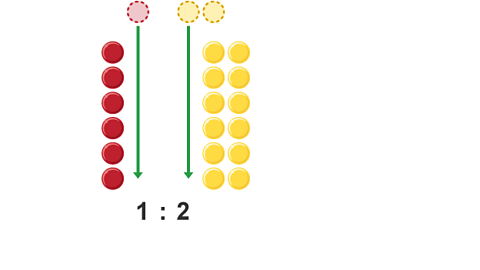
Image caption, This shows that a ratio of 6:12 can simplify to 1:2
1 of 7
Simplify these rations fully:
- \(4:6\)
- \(9:12\)
- \(5:10:15\)
- Divide both numbers by 2: \(4:6=2:3\)
- Divide both numbers by 3: \(9:12=3:4\)
- Divide all numbers by 5: \(5:10:15=1:2:3\)
Simplifying more difficult ratios
Ratios with decimals
To simplify a ratio with a decimal:
- multiply the numbers to make them all whole numbersAny number which does not need a decimal point. Also known as an integer.
- divide both numbers by the highest common factor (HCF) The largest factor that will divide into the selected numbers. Eg, 10 is the highest common factor of 30 and 20. Highest common factor is written as HCF.
Example
Simplify \(6:1.5\).
Solution
Multiply both numbers by 2:
- \(6:1.5\times2=12:3\)
Divide both numbers by 3:
- \(12:3\div3=4:1\)
Ratios with factions
To simplify a ratio with fractions:
- convert the fractions so they have a common denominatorA denominator that is the same for two or more fractions.
- multiply both fractions by the common denominator
- simplify by dividing by the highest common factor
Example
Simplify \(\frac{1}{2}:\frac{3}{4}\)
Solution
Convert so the fractions have a common denominator:
\(\frac{1}{2}:\frac{3}{4}\rightarrow\frac{2}{4}:\frac{3}{4}\)
Multiply by 4:
\(\frac{2}{4}:\frac{3}{4}\times 4=2:3\)
The highest common factor is 1 so this is the simplest form.
Ratios in different units
To simplify ratios that are in different units:
- convert the larger unit to the smaller unit
- simplify the ratio as normal
Example
Simplify \(25mm:5cm\).
Solution
Convert centimetres into millimetres by multiplying by 10:
\(5\text{cm}\times 10 = 50\text{mm}\)
\(25:50\)
Simplify by dividing by 25:
\(1:2\)
Ratios as fractions
Ratios can be used to show fractions and proportionA part-to-whole comparison. Where each part of a ratio is considered as a fraction of the whole. Eg, in the ratio 3 : 5, the first part is 3⁄8 of the whole. This is a proportion of the whole. of amounts.
Example
A room has to be painted blue and yellow in the ratio \(2:3\). Express the proportion of the room that has to be painted in each colour as a fraction.
Solution
There are five parts in this ratio: \(2 \text{blue} + 3 \text{yellow} = 5 \text{total}\)
The fraction painted blue is \(\frac{2}{5}\) and the fraction painted yellow is \(\frac{3}{5}\).
Sharing in a given ratio
Lots of things in everyday life are shared in ratioA relationship between two quantities eg 1:20000. Money is shared, liquids are mixed and teams are assigned using ratios.
Drawing a diagram to represent the ratio can make these tasks easier.
Example
James and Helen get pocket money in the ratio \(3:5\). The total amount of pocket money they are given is £24. How much money do they each get?
Solution
The amount is divided into 8 equal parts since \(3+5=8\). Draw a rectangle with 8 sections and divide it in the ratio \(3:5\), labelling the two parts with the names James and Helen.
Since James’s name comes first he gets three of the parts as the 3 is the first number in the ratio. Helen gets 5 parts, since her name is second.
Share the £24 between the 8 parts by dividing 24 by 8 and put the amount into each part of the diagram.
\(24\div8=3\)
The diagram shows that:
- James gets \(3\times \pounds 3 = \pounds 9\)
- Helen gets \(5\times \pounds 3 = \pounds 15\)
This can also be done when fractions are involved.
Example
To make pink paint, red and white paint can be mixed in the ratio \(1:2\). If you need to make 4 litres of paint, how much red and white paint would you need?
Solution
The ratio has \(1+2=3\) parts.
4 divided by 3 \(3=\frac{4}{3}\)
Each part is worth \(\frac{4}{3}\) litres.
The diagram shows that:
the amount of red paint needed is \(\frac{4}{3} /times 1 = \frac{4}{3} \text{litres}\). This can be written as \(1\frac{1}{3} \text{litres}\)
the amount of white paint needed is \(\frac{4}{3} /times 2 = \frac{8}{3} \text{litres}\). This can be written as \(2 \frac{2}{3} \text{litres}\)
Finding unknown ratios
Using a diagram can help to answer problems when one or more ratios are incomplete or unknown.
Example
Some boys and girls are divided into teams in the ratio \(3:4\). There are 8 girls in one team. How many boys are there in the team?
Solution
There are 8 girls shared into 4 parts. Each part has \(\frac{8}{4}=2\text{girls}.
Fill in the diagram using this information.
Now because the amounts are shared equally between all of the parts, the rest of the table can be filled in.
From the table it is clear that the number of boys in the team is \(2 \times 3 = 6\)
Test yourself
More on M5: Number & Algebra
Find out more by working through a topic
- count2 of 2