Key points about factorising expressions

Factorising is the reverse process of expandExpanding a brackets means multiplying everything inside the bracket by the letter or number outside the bracket to remove the brackets, eg 3(𝑚 + 7) = 3 × 𝑚 + 3 × 7 = 3𝑚 + 21. brackets.
quadraticDescribing an expression of the form 𝒂𝒙² + 𝒃𝒙 + 𝒄 where 𝒂, 𝒃 and 𝒄 are real numbers. expressions contain 𝑥² and can be factorised into two brackets.
Higher - More complex quadratic expressions that have a coefficientA number or symbol multiplied with a variable or an unknown quantity in an algebraic term, eg 5 is the coefficient of 5𝒏. of 𝑥² higher than 1, such as 2𝑥² + 13𝑥 + 15 can also be factorised into two brackets.
Support your understanding of factorising quadratics by looking at these guides on simplifying expressions and expanding double brackets and calculating with negative numbers.
Check your understanding
How to factorise expressions
Factorise (algebra)To write an expression as the product of its factors. For example, 6𝒏 – 12 can be factorised as 6(𝒏 – 2). 𝒙2 + 7𝒙 + 10 can be factorised as (𝒙 + 5)(𝒙 + 2). is the reverse process of expandExpanding a brackets means multiplying everything inside the bracket by the letter or number outside the bracket to remove the brackets, eg 3(𝑚 + 7) = 3 × 𝑚 + 3 × 7 = 3𝑚 + 21. brackets. A factorised answer will always contain a set of brackets.
To factorise an expressionA mathematical sentence expressed either numerically or symbolically made up of one or more terms, eg 8 + 2, or 6𝑥, or 5𝑥² + 3𝑦, or 3𝑎𝑏𝑐. fully, take the Highest Common Factor (HCF)The greatest factor that will divide into the selected numbers. 10 is the highest common factor of 30 and 20. (HCF) of all the terms and put this outside a bracket. This could be the highest number that will go into each term, but it could also contain one or more variableA quantity that can take on a range of values, often represented by a letter, eg 𝑛, 𝑥, 𝑦, 𝑧, 𝑡 … etc. .
Follow the working out below
GCSE exam-style questions

- Fully factorise 20𝑑𝑒 + 5𝑑.
5𝑑 (4𝑒 + 1)
The highest common factor of the two terms is 5𝑑. This goes outside the bracket.
To make 20𝑑𝑒, 5𝑑 must be multiplied by 4𝑒.
To make 5𝑑, 5𝑑 must be multiplied by 1.
- Fully factorise 12𝑎𝑏 – 8𝑎 + 4𝑎²𝑏.
4𝑎 (3𝑏 – 2 + 𝑎𝑏)
There are 3 terms to consider:
The highest common factor of all three terms is 4𝑎. This goes outside the bracket.
To make 12𝑎𝑏, 4𝑎 must be multiplied by 3𝑏.
To make –8𝑎, 4𝑎 must be multiplied by –2.
To make 4𝑎²𝑏, 4𝑎 must be multiplied by 𝑎𝑏.
Video – Factorising quadratics when the 𝑥² coefficient is 1.
Watch this video to find out how to factorise quadratics, when the 𝑥² coefficient is 1 using the FOIL and grid methods.
Factorising quadratics when the 𝑥 squared coefficient is 1.
The highest power of 𝑥 in a quadratic expression is 𝑥 squared. A quadratic expression might also have 𝑥 terms and constants, which are just numbers. 𝑥 and 𝑥 squared terms may also have coefficients, which are multipliers, or numbers in front of the ‘𝑥’s. These could be many different types of numbers, including positive or negative or fractional or whole.
In this video, we'll look at quadratics with 𝑥 squared coefficients of 1.
A set of two brackets can be expanded using either the FOIL or grid method. For example, using the grid method, 𝑥 add 2 times 𝑥 subtract 5 equals 𝑥 squared add 2𝑥 subtract 5𝑥 subtract 10. Which simplifies to 𝑥 squared subtract 3𝑥 subtract 10.
For any quadratic with an 𝑥 squared coefficient of 1, the two numbers in the brackets will always add to give the 𝑥-coefficient and multiply to give the constant. So here, 2 add –5 equals –3 and 2 multiplied by –5 equals –10.
This can help you factorise quadratic expressions, which is the opposite of expanding brackets. When factorising, we put the quadratic into brackets and express it as its factors. When expanding, we multiply out and remove the brackets.
Let's look at some example questions.
Factorise 𝑥 squared add 7𝑥 add 12.
First, you need to find two numbers that add to 7 and multiply to give 12. Start by listing all the factor pairs of 12. These are 1 and 12, 2 and 6, and 3 and 4.
1 add 12 equals 13 and 2 add 6 equals 8, so these aren't correct. 3 add 4 equals 7, which matches the 𝑥-coefficient so this is the correct pair of numbers. So, 𝑥 squared add 7𝑥 add 12 can be factorised as 𝑥 add 3 times 𝑥 add 4. You can expand the brackets again to check your answer.
For the next question, factorise 𝑥 squared subtract 8𝑥 add 15.
Why not pause the video and have a go at this one?
This time, look for numbers that add to –8 and multiply to give 15. With this one, the constant is positive but the 𝑥-coefficient is negative, so you need to look at the negative factor pairs of 15. These are –1 and –15, and –3 and –5. –3 add –5 equals –8, which is the 𝑥-coefficient.
So, 𝑥 squared subtract 8𝑥 add 15 equals 𝑥 subtract 3 times 𝑥 subtract 5.
Remember to always expand the brackets again to check your answer.
Factorising quadratics into two brackets
This is a quadratic expressionA mathematical sentence made up of one or more terms expressed either numerically or symbolically. where 𝑥 is the variableA symbol for an unknown value. It is usually a letter like 𝒙 or 𝒚.:

In a quadratic expression, 𝑥² is the highest power of 𝑥.
𝑎 and 𝑏 are coefficientA number or symbol multiplied with a variable or an unknown quantity in an algebraic term, eg 5 is the coefficient of 5𝒏. and 𝑐 is a constantA number that does not vary. Constants are different to variables such as 𝑥 and 𝑦 that can take many values. . 𝑎𝑥², 𝑏𝑥 and 𝑐 are termsAn element within an algebraic sentence. Elements (terms) are separated by + or - signs..
In Foundation Tier, 𝑎 will always be 1, so quadratic expressions will be in the form 𝑥² + 𝑏𝑥 + 𝑐.
Quadratic expressions in the form 𝑥² + 𝑏𝑥 + 𝑐 do not have a common factorA number or variable that divides exactly into a term. that can be taken outside a bracket. This means they cannot be factoriseTo express a number or an expression as the product of its factors, eg 6 can be factorised as 2 × 3, and 6𝑛 – 12 can be factorised as 6(𝑛 – 2). using one bracket. However, they can sometimes be factorised into two brackets in the form (𝑥 + 𝑝)(𝑥 + 𝑞) where 𝑝 and 𝑞 are integerIntegers are numbers with no fraction or decimal part. They can be positive, negative or zero. 42, -8, and 10,000 are examples of integers. .
Factorising is the reverse process of expandExpanding a brackets means multiplying everything inside the bracket by the letter or number outside the bracket to remove the brackets, eg 3(𝑚 + 7) = 3 × 𝑚 + 3 × 7 = 3𝑚 + 21. brackets:
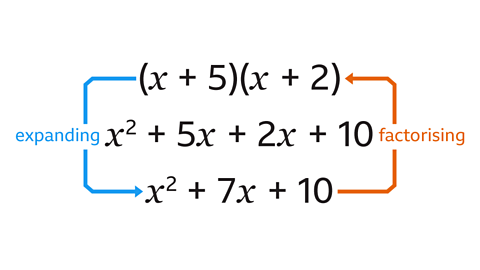
To factorise the quadratic 𝑥² + 𝑏𝑥 + 𝑐, the sumThe answer to an addition calculation. of the two numbers in the brackets must be 𝑏, and the productThe result of multiplying one number by another, eg the product of 4 and 5 is 20 since 4 × 5 = 20.must be 𝑐.
In the example above:
- 5 + 2 = 7 (𝑏)
- 5 × 2 = 10 (𝑐)
Follow the working out below
Video - Factorising quadratic expressions
Watch this video to understand out how to factorise quadratic expressions correctly to avoid losing marks in exams.
Factorising quadratic expressions.
These can be tough, but use this method to minimise losing marks.
The trick with this one is to always double check your answer by multiplying out the brackets and comparing your answer with the original expression you started with.
For example, take the expression 𝑥 squared plus 7𝑥 plus 10. The correct way to find the bracket values is to find two factors of the constant 10, so, two numbers which multiply together to give 10, that also add up to the coefficient of 𝑥, which is 7.
The factors of 10 are 10 and 1, or 5 and 2. As you can see, only one of these pairs adds up to the 𝑥-coefficient 7: 5, and 2. To check your answer is correct, substitute these values into the brackets: 𝑥 plus 2 and 𝑥 plus 5 and multiply out.
Here we'll use the grid method, but you could use any method that you feel comfortable with.
So, multiplying the terms together gives us 𝑥 times 𝑥 which equals 𝑥 squared, 𝑥 times 2 which equals 2𝑥, 5 times 𝑥 which equals 5𝑥, and 5 times 2 which equals 10.
Add all these values together and we have 𝑥 squared plus 7𝑥 plus 10. Notice this is the original expression and shows that the factorisation is correct. But a common mistake in factorising is picking any two factors that multiply to give the constant, like 1 and 10 for 10, and assuming the expression can be written as 𝑥 plus 1, 𝑥 plus 10.
It seems logical because 1 times 10 does equal 10, but factorising isn't just about multiplication. Remember, the numbers also need to add up to match the 𝑥-term coefficient, which in this example is the middle term 7𝑥. If we made this mistake, let's see what happens when we multiply out the brackets to check our answer.
Multiplying the terms together gives us 𝑥 times 𝑥 which equals 𝑥 squared, 1 times 𝑥, which gives us 1𝑥 or just 𝑥, 10 times 𝑥 gives us 10𝑥, and finally 1 times 10 gives us 10. Adding up the like 𝑥 terms leaves us with 𝑥 squared plus 11𝑥 plus 10.
As you can see, this isn't the same as the original expression. This is why it's really important when factorising quadratics to remember two things.
One: multiply out the brackets to check your answer and two: compare your answer to the original expression you started with. If it matches, then you've conquered factorising quadratics.
GCSE exam-style questions

- Factorise 𝑥² + 12𝑥 + 20.
(𝑥 + 2)(𝑥 + 10)
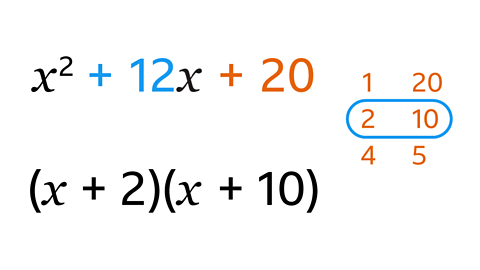
- List pairs of numbers that multiply to make 20.
- Find the pair that adds to make 12.
- 2 and 10 multiply to make 20, and add to make 12.
- These are the numbers that go into the brackets. (𝑥 + 10)(𝑥 + 2) would also be correct.
- Factorise 𝑥² – 4𝑥 – 21.
(𝑥 + 3 )(𝑥 – 7)
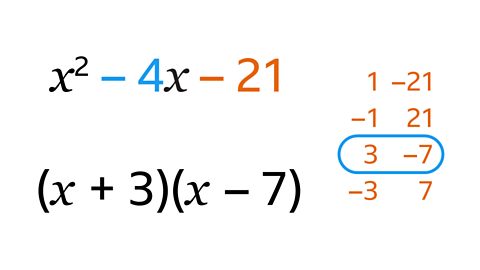
- List pairs of numbers that multiply to make –21.
- A positive number and a negative number will multiply to give a negative answer.
- Find the pair that add to make –4.
- 3 and –7 multiply to make –21, and add to make –4.
- These are the numbers that go into the brackets.
(𝑥 – 7)(𝑥 + 3) would also be correct.
- Factorise 𝑥² – 49.
(𝑥 + 7)(𝑥 – 7)

This is an example of a difference of two squares.
- The square rootA value that, when multiplied by itself, gives the number, eg 4 × 4 = 16, so the square root of 16 is 4, √16 = 4. of 49 is 7.
- The numbers required are 7 and –7. (𝑥 – 7)(𝑥 + 7) would also be correct.
Quiz - Factorising expressions
Practise what you've learned about factorising expressions with this quiz.
Higher - Factorising quadratics where 𝑎 > 1
Factorising quadratic expressions of the form 𝑎𝑥² + 𝑏𝑥 + 𝑐 where 𝑎 is greater than 1 requires a different method to those where 𝑎 = 1.
Follow the working out below
GCSE exam-style questions
- Factorise 6𝑥² – 7𝑥 – 3.
(2𝑥 – 3)(3𝑥 – 1)
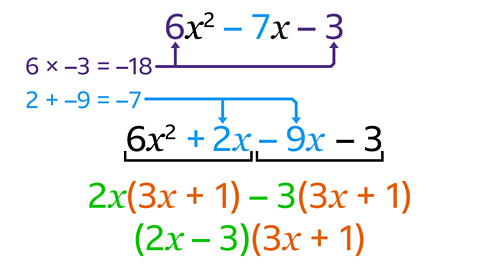
- Multiply the coefficient of 𝑥² (6) by the constant term (–3) to make –18.
- Find a pair of numbers that multiply to make –18 and add together to make –7.
- The numbers are 2 and –9.
- Rewrite the 𝑥 term so that –7𝑥 becomes 2𝑥 – 9𝑥.
- Factorise 6𝑥² + 2𝑥 and – 9𝑥 – 3.
- Make sure the bracket created is the same for each.
- Altogether there are 2𝑥 – 3 lots of (3𝑥 – 1).
- The answer is (2𝑥 – 3)(3𝑥 – 1).
- Factorise 6𝑥² + 13𝑥 + 5.
(3𝑥 + 5)(2𝑥 + 1)

Multiply the coefficientA number or symbol multiplied with a variable or an unknown quantity in an algebraic term, eg 5 is the coefficient of 5𝒏. of 𝑥² (6) by the constantThe number or quantity that does not vary. In the expression 𝒙2 + 3𝒙 + 6, the 6 is a constant, whereas 𝒙 is a variable. term (5) to make 30.
- Find a pair of numbers that multiply to make 30 and add together to make 13.
- The numbers are 3 and 10.
- Rewrite the 𝑥 term so that 13𝑥 becomes 3𝑥 + 10𝑥.
- Factorise 6𝑥² + 3𝑥 and 10𝑥 + 5.
- The bracket created should be the same in each factorisation.
- Altogether there are 3𝑥 + 5 lots of (2𝑥 + 1).
- The answer is (3𝑥 + 5)(2𝑥 + 1).
Higher - Quiz - Factorising expressions
Practise what you've learned about factorising expressions with this quiz for Higher tier.
Now that you have revised factorising expressions, why not look at sequences?
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Algebra
Find out more by working through a topic
- count3 of 14
- count4 of 14

- count5 of 14
- count6 of 14
