Key points about equations with brackets, fractions and unknowns

Solving an equation means finding the value of an unknown variableA quantity that can take on a range of values, often represented by a letter, eg 𝑛, 𝑥, 𝑦, 𝑧, 𝑡 … etc. (usually 𝑥) so that the equationA mathematical statement showing that two expressions are equal. The expressions are linked with the symbol =. is true.
Some equations have brackets, such as 3(𝑥 + 5) = 21. expandExpanding means to multiply to remove the brackets. these brackets makes the equation easier to solve.
An equation can have 𝑥 term (algebra)An element within an algebraic sentence, eg 𝑥 or 5𝑦 or 3𝑒². Elements (terms) are separated by + or – signs. on both sides, for example 5𝑥 – 4 = 2𝑥 – 11.
Make sure you are confident in solving one and two-step linear equations and expanding brackets in order to tackle these more complex types of equations.
Check your understanding
Solving equations with brackets
Some equations include a set of brackets, such as 2(11 − 3𝑥) = 4. To solve equationA mathematical statement showing that two expressions are equal. The expressions are linked with the symbol =. with brackets, the most common first step is to expandExpanding means to multiply to remove the brackets. the bracket.
Expanding a bracket does not change the value of an expressionA mathematical sentence expressed either numerically or symbolically made up of one or more terms, eg 8 + 2, or 6𝑥, or 5𝑥² + 3𝑦, or 3𝑎𝑏𝑐. . It is another way of writing the same expression.
To solve the expanded equation, use inverse operationThe opposite of a mathematical process. For example, the inverse of × 5 is ÷ 5. The inverse operation undoes the original process. to isolateRearranging an equation so that one variable is on its own on one side of the equation. the 𝑥 term, and find the value of 𝑥.
substituteIn algebra, to replace a letter with a number. the value of 𝑥 back into the original equation to check the answer is correct.
Follow the working out below
Some equations have negative 𝑥 term (algebra)An element within an algebraic sentence, eg 𝑥 or 5𝑦 or 3𝑒². Elements (terms) are separated by + or – signs.. Manipulate both sides to make the 𝑥 terms positive. This makes the equation easier to solve.
Follow the working out below
GCSE exam-style questions
- Solve the equation 3(2𝑥 + 4) = 36.
𝒙 = 4
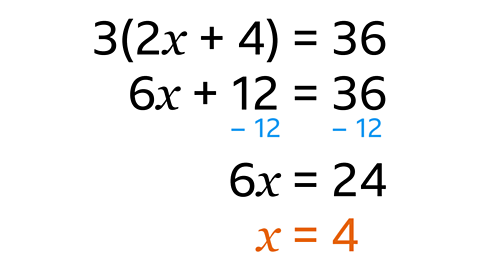
- Expand the brackets to give the new equation of:
6𝑥 + 12 = 36.
- Isolate the 𝑥 term by subtracting 12 from each side.
This gives 6𝑥 = 24.
- Divide both sides by 6.
This gives a solution of 𝑥 = 4.
- Check the solution by substituting 4 back into the original equation.
3(2 × 4 + 4) = 3(8 + 4) = 3 × 12 = 36.
The left-hand side and the right-hand side both equal 36, so 𝑥 = 4 is correct.
- Solve the equation 4(𝑥 – 2) + 3(𝑥 + 1) = 16.
𝒙 = 3
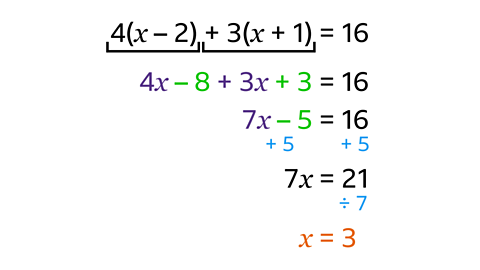
- Expand the brackets separately to give the new equation of:
4𝑥 – 8 + 3𝑥 + 3 = 16
- Simplify the left-hand side by collecting the 𝑥 terms and the number terms to give:
7𝑥 – 5 = 16
- Isolate the 𝑥 term by adding 5 to each side.
This gives 7𝑥 = 21.
Divide both sides by 7. This gives a solution of 𝑥 = 3.
Check the solution by substituting 3 back into the original equation.
4(3 – 2) + 3(3 + 1) = 4 × 1 + 3 × 4 = 4 + 12 = 16
The left-hand side and the right-hand side both equal 16, so 𝑥 = 3 is correct.
Solving equations with unknowns on both sides
Video – Solving equations
Watch this video to find out how to solve equations with unknowns on both sides, using number and algebra discs.
Solving equations.
When solving equations, number and algebra discs can be used to represent positive and negative values.
A positive and a negative disc of the same kind added together form a zero pair. That's because they cancel each other out completely to equal zero. Creating zero pairs can help you isolate variables and solve equations. In this case, isolating variables just means getting all the 𝑥 terms on one side of the equation.
Let's try a question.
Solve 8𝑥 add 5 equals 2𝑥 subtract 19.
Start by representing each value with discs. There are 8 positive 𝑥 discs and 5 positive 1 discs on the left-hand side and 2 positive 𝑥 discs and 19 negative 1 discs on the right-hand side.
To solve this equation, you need to isolate the variable on one side, or in other words, 𝑥 should appear on one side of the equals sign only.
Notice that there are fewer 𝑥 discs on the right-hand side. You can cancel these out by adding 2 negative 𝑥 discs to both sides of the equation. Creating two zero pairs on each side.
Remember, equations need to stay balanced, so whatever you do to one side, you must also do to the other.
This leaves no 𝑥 discs on the right-hand side and 6 positive 𝑥 discs on the left-hand side. So 6𝑥 add 5 equals –19. Then, to isolate the 𝑥 term further, you need to remove 5 from the left-hand side. This means adding 5 negative 1 discs to both sides, forming 5 zero pairs on the left-hand side, which all cancel to give 6 𝑥 discs and 24 negative 1 discs on the right-hand side.
So, 6𝑥 equals –24. To finish solving the equation, you need to find the value of 𝑥. If 6𝑥 equals –24 then dividing both sides by 6 will give you the answer: 𝑥 equals –4.
equationA mathematical statement showing that two expressions are equal. The expressions are linked with the symbol =. need to stay balanced on both sides of the equals sign. Whatever is done to one side of the equation must also be done to the other.
Equations are easier to solve when the unknown variableA quantity that can take on a range of values, often represented by a letter, eg 𝑛, 𝑥, 𝑦, 𝑧, 𝑡 … etc. (usually 𝑥) is just on one side, but sometimes there are 𝑥 term (algebra)An element within an algebraic sentence, eg 𝑥 or 5𝑦 or 3𝑒². Elements (terms) are separated by + or – signs. on both sides.
To create a simpler equation where the 𝑥 terms are on one side only, subtract the lowest 𝑥 term from both sides. Doing this means that negative 𝑥 terms are avoided.
If the lowest 𝑥 term is negative, subtracting this negative term is the same as adding a positive term.
Follow the working out below
GCSE exam-style questions
- Solve 4𝑥 – 7 = 𝑥 + 8.
𝒙 = 5
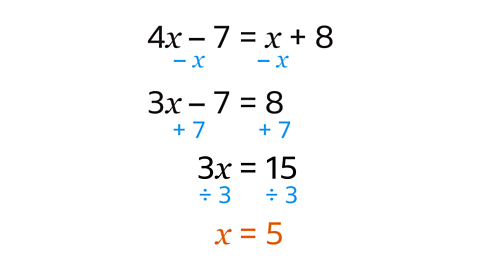
𝑥 is the lowest 𝑥 term. Subtract 𝑥 from both sides to give 3𝑥 – 7 = 8. The number terms stay the same.
Add 7 to both sides to isolate 𝑥.
This gives 3𝑥 = 15.
- Divide both sides by 3 to reach the solution 𝑥 = 5.
- Solve 4𝑥 + 3 = 9 – 2𝑥.
𝒙 = 1
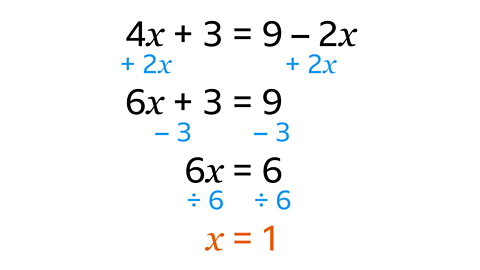
–2𝑥 is the lowest 𝑥 term. This is a negative term, so add 2𝑥 to both sides to give 6𝑥 + 3 = 9. The number terms stay the same.
Subtract 3 from both sides to isolate 𝑥.
This gives 6𝑥 = 6.
- Divide both sides by 6 to reach the solution 𝑥 = 1.
Solving equations with fractions
Solving an equationA mathematical statement showing that two expressions are equal. The expressions are linked with the symbol =. requires the use of inverse operationThe opposite of a mathematical process. For example, the inverse of × 5 is ÷ 5. The inverse operation undoes the original process. .
In a fraction, the numeratorNumber written at the top of a fraction. The numerator is the number of parts used, eg for ⅓, the numerator is 1. is divided by the denominatorNumber written on the bottom of a fraction. The denominator is the number of equal parts, eg for ⅓, the denominator is 3..
The inverse operation is to multiply by the denominator.
Doing this to both sides of an equation removes the fraction and makes the equation easier to solve.
Follow the working out below
GCSE exam-style questions
- Solve the equation.
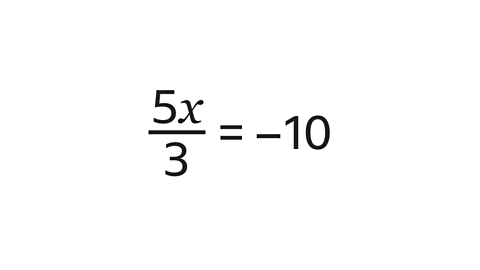
𝒙 = –6
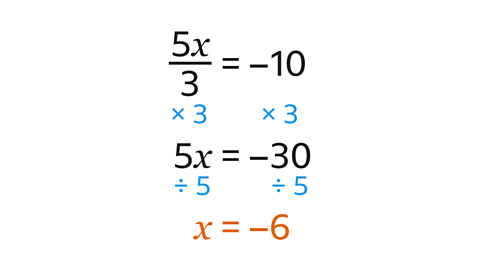
Multiply both sides by 3 to remove the fraction. This makes 5𝑥 = –30.
Divide both sides by 5 to give the solution 𝑥 = –6.
- Solve the equation.
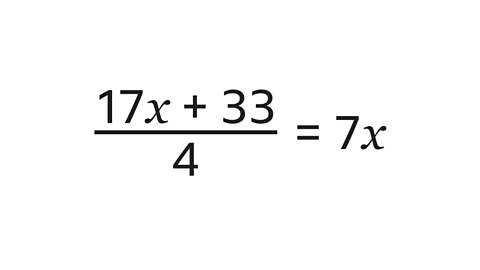
𝒙 = 11
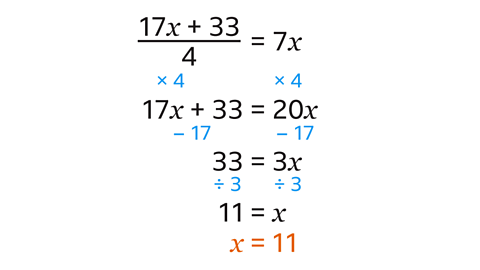
Multiply both sides by 4 to remove the fraction.This makes 17𝑥 + 33 = 20𝑥.
There are 𝑥 terms on both sides of the equation. The lowest 𝑥 term is 17𝑥. Subtract 17𝑥 from both sides so that there are 𝑥 terms on just one side. This makes 33 = 3𝑥.
Divide both sides by 3 to give the solution 𝑥 = 11.
Quiz – Solving more complex linear equations
Practise what you've learned about solving more complex linear equations with this quiz.
Higher – Video – Solving equations with fractions
Watch this video for Higher tier to find out more on how to solve equations that include fractions.
Solving equations with fractions – Higher tier.
When solving an equation where one side is a fraction, it’s a good idea to start by multiplying both sides by the denominator. This removes the fraction and gives an equation that you can solve in the usual way.
Remember, when solving equations, whatever you do on one side, you must do on the other side too, to keep the equation balanced.
If the equation you're solving has two fractions, for example 𝑥 over 2, add 3𝑥 over 4, equals 5, start by finding a common denominator. 4 is a multiple of 2, so you can multiply the numerator and denominator of the first fraction by 2, giving an equivalent fraction with denominator 4.
Now that both fractions have the same denominator, you can rewrite them as one fraction with denominator 4. If you multiply both sides of the equation by 4, 4 will cancel out on the left-hand side, giving 2𝑥 add 3𝑥 equals 20.
Then you can solve in the usual way. So, add like terms on the left-hand side to get 5𝑥 equals 20, and then divide both sides by 5 to get 𝑥 completely on its own.
So, 𝑥 equals 4.
Let's look at another example.
Solve the equation 4𝑥 subtract 5, all over 5, add 𝑥 add 4, all over 2, equals 14.
It will be easier to solve this equation if the two separate fractions are written as one. So, first find the common denominator so that you can add the fractions.
The smallest number that has factors of both 5 and 2 is 10. So multiply the numerator and denominator of the first fraction by 2 and the numerator and denominator of the second fraction by 5. 2 multiplied by 5 equals 10, so both fractions now have the same denominator.
Next, let's simplify the numerator. First, expand the brackets: 2 multiplied by 4𝑥 equals 8𝑥, 2 multiplied by –5 equals –10, 5 multiplied by 𝑥 equals 5𝑥, and 5 multiplied by 4 equals 20.
Then, you need to simplify the expression in the numerator by collecting like terms. 8𝑥 and 5𝑥 are like terms, so they can be added to give 13𝑥. Likewise, –10 add 20 equals 10, giving 13𝑥 add 10, all over 10, equals 14.
Now multiply both sides of the equation by 10 to remove the fraction completely. On the left-hand side, 10 cancels with the denominator to give 13𝑥 add 10 equals 14 times 10. 14 times 10 equals 140, so this gives 13𝑥 add 10 equals 140.
You can now solve this equation in the usual way. Subtract 10 from both sides of the equation to remove 10 from the left-hand side. This means the 𝑥 term is now on its own on one side of the equation. Then, 140 subtract 10 equals 130, which means 13𝑥 equals 130.
Finally, divide both sides of the equation by 13 to give 𝑥 equals 130 over 13. 130 divided by 13 equals 10, so the solution is 𝑥 equals 10.
Now you have revised solving equations with brackets, fractions and unknowns on both sides, why not take a look at accuracy in maths?
More on Algebra
Find out more by working through a topic
- count8 of 14
- count9 of 14
- count10 of 14

- count11 of 14