Key points about sequences
A number sequence is a list of ordered numbers that follow a pattern or a rule. A term-to-term rule explains how to find the next A value in a sequence. The 3rd term is the 3rd value in the sequence. of a sequence.
The πth term of a sequence is a βposition-to-term rule that can be used to find out any term in a sequence.
The πth term of an A sequence that increases or decreases by the same number each time, eg 4, 7, 10, 13. Sometimes called a linear sequence.Β (sometimes known asβ aβ βlinearβ sequence) is found by comparing the sequence to an appropriate times table.
Higher tier - The πth term of a Describing an expression of the form ππ₯Β² + ππ₯ + π where π, π and π are integers. sequence is found by considering the Once the first difference between values of a sequence is calculated, the second difference is the difference between these values.Β between the terms and comparing the sequence to another that contains πΒ².
Check your understanding
Term-to-term rules
A sequence is a list of values that follow a rule. Each value is called a term.
A rule that explains how to find the next term in a sequence is called a term-to-term rule.
The most common type of sequence is an arithmetic (or linear) sequence. The difference between each term is the same every time, and is known as the common difference.
Follow the working out below
GCSE exam-style questions
- β20, β17, β14, β11 are the first four terms of a sequence. Find the term-to-term rule.
The term-to-term rule is βadd 3β.
The negative numbers are getting closer to zero and the terms are increasing by 3 each time.
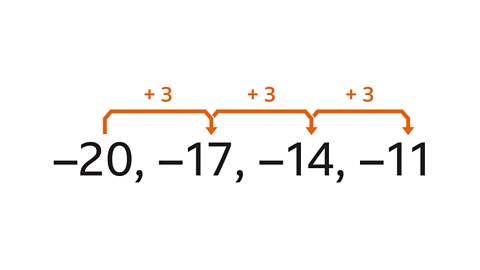
- The term-to-term rule of a sequence is βmultiply by 5, then subtract 3β. The first term is 2. Work out the 3rd term.
The third term is 32
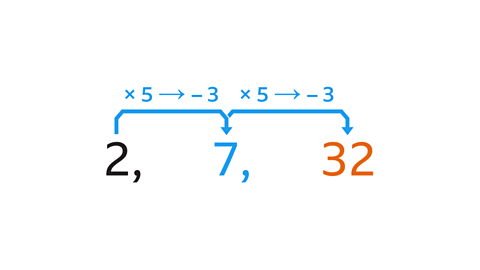
To work out the second term, multiply the first term by 5, then subtract 3.
2 Γ 5 β 3 = 7β.β
To work out the third term, multiply the second term by 5, then subtract 3.
7 Γ 5 β 3 = 32β.β
- The term-to-term rule of a sequence is βadd 3 then multiply by 2β. The third term is 46. Calculate the first term.
The first term is 7.
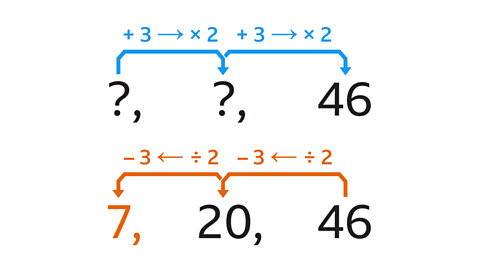
- To calculate the second term, work backwards from the third term. The term-to-term rule in reverse is βdivide by 2, then subtract 3β.ββ
46 Γ· 2 = 23. Then 23 β 3 = 20. The second term is 20.
- To calculate the first term, work backwards from the second term. Use the same term-to-term rule in reverse.
20 Γ· 2 = 10. Then 10 β 3 = 7. The first term is 7.
πth term rules
Rather than finding the next term or next two terms of a sequence, it may be necessary to work out the 50th term, for example.
To do this without writing out all 50 terms, a general rule called the πth term is found.
To find an A mathematical sentence expressed either numerically or symbolically made up of one or more terms, eg 8 + 2, or 6π₯, or 5π₯Β² + 3π¦, or 3πππ. for the πth term of an A sequence that increases or decreases by the same number each time, eg 4, 7, 10, 13. Sometimes called a linear sequence.Β , work out the The difference between each term in an arithmetic linear sequence. between the terms and treat the sequence as a times table that has been shifted.
- For example, 3, 7, 11, 14 has a common difference of 4, and is the 4 times table with 1 subtracted. The πth term is therefore 4π β 1.
To find the 50th term, In algebra, to replace a letter with a number. the value of 50 into the πth term rule.
Follow the working out below
GCSE exam-style questions
- A linear sequence starts 3, 8, 13, 18, 23. Work out an expression for the πth term.
5π β 2
Write the numbers for π above the sequence.
The common difference between the terms is 5, βso write the 5 times table under βClick here to enter text.ββ the values of πβ. Label the 5 times table as 5π.
Work out how to get from the 5π row to the sequence. The sequence is the 5 times table subtract 2. The πth term is 5π β 2.
- An arithmetic sequence starts 14, 11, 8, 5, 2. Work out an expression for the πth term.
β3π + 17
- Write the numbers for π above the sequence.
- The common difference is β3, so write the β3 βtimes tableβ under the values of π. Label the row as β3π.
- Work out how to get from the β3π row to the sequence. The β3π row has had 17 added.
The πth term is β3π + 17.
(Another way to write the answer is 17 β 3π).
- βWrite down the first three terms of a sequence where the πth term is given by πΒ² + 5.
6, 9, 14
β1. The first term is when π = 1. Substitute 1 into πΒ² + 5 to give 12 + 5 = 6.
- βThe second term is when π = 2. Substitute 2 into πΒ² + 5 to give 22 + 5 = 9.
β3. The third term is when π = 3. Substitute 3 into πΒ² + 5 to give 32 + 5 = 14.
β4. The first three terms are 6, 9, 14.
β(Note: this sequence is not an arithmetic sequence as it does not go up by the same number each time.)
Quiz β Sequences
Practise what you have learned about sequences with this quiz.
Higher β πth term of a quadratic sequence
Quadratic sequences have an πth term rule that contains πΒ².
Follow the working out below
Example 1
Example 2
The differences between the terms are not equal, but the Once the first difference between values of a sequence is calculated, the second difference is the difference between these values.Β between the terms are equal.
To find the πth term, follow these steps:
Work out the first differences between the terms. The first differences are not the same. Work out the second differences.
The second differences will be the same. The A number or symbol multiplied with a variable or an unknown quantity in an algebraic term. For example, 4 is the coefficient of 4nΒ². (π) of πΒ² in the πth term rule is always half of the second difference.
Compare the numbers of the sequence ππΒ² with the original quadratic sequence. The difference between them will be a A number that does not vary. Constants are different to variables such as π₯ and π¦ that can take many values.Β , or should make an A sequence that increases or decreases by the same number each time, eg 4, 7, 10, 13. Sometimes called a linear sequence.Β .
Add the constant or πth term for the arithmetic sequence to ππΒ² to give the πth term for the quadratic sequence.
GCSE exam-style questions
- A quadratic sequence has an πth term of 2πΒ² + 4π β 3. Find the first 3 terms.
3, 13, 27
Substitute π = 1 into the expression. The first term is 2(1Β²) + 4(1) β 3 = 2(1) + 4 β 3 = 3
Substitute π = 2 into the expression. The second term is 2(2Β²) + 4(2) β 3 = 2(4) + 8 β 3 = 13
Substitute π = 3 into the expression. The third term is 2(3Β²) + 4(3) β 3 = 2(9) + 12 β 3 = 27
- Work out the πth term of the sequence 6, 9, 14, 21, 30.
πΒ² + 5
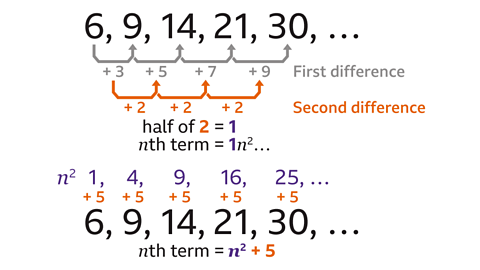
The first differences are + 3, + 5, + 7, + 9.
The second differences are all +2. Half of 2 is 1, so the coefficient of πΒ² is 1.
Write the values of 1πΒ² and compare it to the sequence. The constant value of 5 is always added to πΒ² to make the sequence.
Write the final πth term rule as πΒ² + 5.
- Work out the ββπββth term of the sequence 3, 9, 17, 27, 39.ββ
ββπββΒ² + 3ββπββ βββ 1
The first differences are + 6, + 8, + 10, + 12. ββ
The second differences are all + 2. Half of 2 is 1, so the coefficient of ββπββΒ²ββ is 1.ββ
Write the values of ββ1πββΒ²ββ and compare it to the sequence. The differences 2, 5, 8, 11, 14 form an arithmetic sequence whose πth term is ββ3π β1ββ (the 3 times table subtract 1).ββ
Add 3π β 1 to πββΒ²ββ to give the final πth term rule
ββπββΒ² + 3πββ βββ 1.ββββ
Quadratic sequences β interactive activity
This interactive activity will help you to learn how to create quadratic sequences by selecting different coefficient values.
Higher β Quiz β Sequences
Practise what you have learned about sequences with this quiz for Higher tier.
Now that you have revised sequences, why not try looking at geometric and special sequences?
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.
More on Algebra
Find out more by working through a topic
- count11 of 14
- count12 of 14
- count14 of 14
