Module 3 (M3) - Algebra - Factorising

Part ofMathsM3: Algebra

Factorising quadratic expressions

Factorising an expression means finding the factors that multiply together to give that expression.

A quadratic expression is one that has an ‘𝓍²’ term as its highest power.

\(\mathbf {x^2}\), \(\mathbf {2x^2 -3x}\), \(\mathbf {x^2 - 9}\) and \(\mathbf {x^2 + 5x + 6}\) are all quadratic expressions.

Some quadratic expressions cannot be factorised.

Back to top

Factorising quadratic expressions of the form \(\mathbf {x^2 + bx + c}\)

To find a method for factorising an expression such as \(\mathbf {x^2 + 5x + 6}\), look at how that expression was arrived at by expanding two brackets.

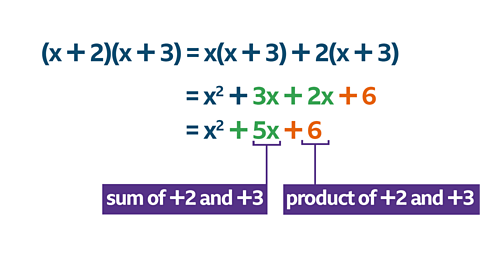
(x + 2)(x + 3) = x(x + 3) + 2(x + 3) = x2 + 3x + 2x + 6 = x2 + 5x + 6

There are three terms in the expanded expression:

First term:
𝓍²

Second term:
sum of +2𝓍 and +3𝓍

Third term:
product of +2 and +3

This information gives us a method for factorising.

Back to top

Examples

Factorise \(\mathbf {x^2 + 2x – 15}\):

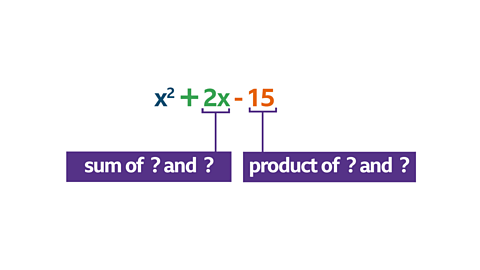
To Factorise:

  • Find two numbers whose sum is +2 and whose product is –15

The product is minus 15, so one of factors must be negative.

The numbers needed are either:

+5 and -3 or -5 and +3 As the sum is positive, the pair with the higher + value is the one to choose i.e.
+5 and -3

  • Write down the factors:

\(\mathbf {x^2 + 2x – 15 = (x + 5)(x – 3)}\)

  • Answer:
    \(\mathbf {x^2 + 2x – 15 = (x + 5)(x – 3)}\)
    \(\mathbf {(x - 3)(x + 5)}\) is also a correct answer. The order of the factors does not matter.
Back to top

Question

Factorise \(𝓍² + 5𝓍 – 24\)

Back to top

E𝓍ample

Factorise 𝓍² - 9𝓍 + 20

Solution

Identify the product and sum of the two key values that we need to find.

  • Product = +20

  • Sum = - 9
    -4 and -5 add to give -9 and multiply to give +20

  • The factors are (𝓍 - 4) and (𝓍 - 5)

Answer:𝓍² - 9𝓍 + 20 = (𝓍 - 4)(𝓍 - 5)

Back to top

Question

Factorise x² - 17x + 70

Back to top

Factorising expressions of the form 𝓍²-a² (difference of two squares)

Expressions such as 𝓍²-a² can be factorised using the difference of two squares method.

To understand how this works, look at the result when (𝓍 + 5)(𝓍 – 5) is expanded.

(𝓍 + 5)(𝓍 – 5) = 𝓍(𝓍 -5) + 5(𝓍 – 5)= 𝓍² – 5𝓍 + 5𝓍 – 25 Since = 𝓍²– 25 Expanding (𝓍 + 5)(𝓍 – 5) gives 𝓍² – 25

The inverse of this means that 𝓍² – 25 factorises to give (𝓍 + 5)(𝓍 – 5)

  • Note that in the expression 𝓍² – 25 𝓍 is squared
  • 25 = 5² and there is a minus sign in between so we have the difference of two squares!

In general, 𝓍² – a² can be factorised to give (𝓍 + a)(𝓍 – a)

Back to top

Both 𝓍² and 100 (10²) are squares and there is a - sign in between.

Use the difference of two squares method - DOTS.

The factors can be written down without any further working.

𝓍² – 100 = 𝓍² – 10²

= (𝓍 + 10)(𝓍 – 10)

Back to top

Question

Factorise 𝓍² - 49

Back to top

Example

Factorise 9 - 𝓍²

DOTS can still be used here – the expression does not have to start with ‘𝓍²”

9 - 𝓍² = 3² - 𝓍²

Factors are (3 + 𝓍)(3 – 𝓍)

Answer:
9 - 𝓍² = (3 + 𝓍)(3 – 𝓍)

Difference of two squares (DOTS) often appears on exams

Back to top

Test yourself

Back to top

More on M3: Algebra

Find out more by working through a topic