Module 8 (M8) - Algebra - Simultaneous equations

Simultaneous equations are two or more equations with two or more variables. They are simultaneous because they can be solved to give values for the variables that are equal in each equation.

It may be useful to look at M4 Quadratic Equations, M4 Algebraic Fractions, M6 Simultaneous equations and M7 Simultaneous Equations.

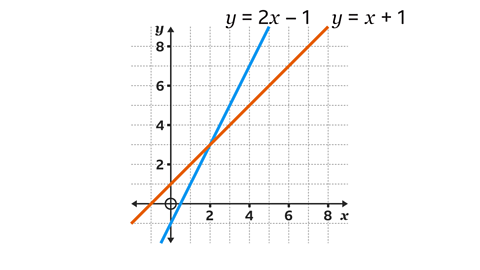
The solution to the equations:
y = 2𝑥 - 1 and y = 2𝑥 - 1
Is when 𝑥 = 2 and 𝑦 = 3(2, 3)

In the paper, one of the equations will be linear and the other non-linear, e.g. quadratic.

There are 3 common styles of question.

1. Both equations are given in the form 𝑦 =
   𝑦 = 𝑥 + 3
   𝑦 = 𝑥² + 3𝑥
2. One equation is given as 𝑦 = and the other is not
   𝑦 = 2𝑥 - 3
   2 = 𝑥² + 𝑦²
3. Neither equation is given in the form 𝑦 =
   𝑥𝑦 = 12
   𝑦 - 3𝑥 + 9 = 0

The most common method for solving linear simultaneous equations is the elimination method. This method can be used for linear and non-linear but looks a little different.

1. Eliminate one of the letters from both equations
2. Calculate the values of the remaining letter - there will usually be two answers.
3. Substitute each value back into one of the equations to find the value of the other letter - there will usually be two pairs of answers.

Example

Solve the following simultaneous equations.

𝑦 = 𝑥 + 3
𝑦 = 𝑥² + 3𝑥

Solution

1. Eliminate one of the letters from both equations by equating the Right Hand Sides (RHS) of the equations.
   
   Since both equations are in the form y = RHS, both Right Hand Sides can be equated or set equal to each other
   𝒙 + 3 = 𝒙² + 3𝒙

2. Calculate the values of the remaining letter.
   
   Simplify the quadratic by taking all the terms to one side and putting it equal to zero and solving to find both values of x - there will be two answers.
   
   𝑥² + 3𝑥 - 𝑥 - 3 = 0
   𝒙² + 2𝑥 - 3 = 0
   (𝑥 + 3)(𝑥 - 1) = 0
   𝑥 = -3 𝑥 = 1

3. Substitute each value back into one of the equations to find the values of the other letter. It doesn’t matter which equation you chose but the linear equation is a sensible choice!
   
   𝑦 = 𝑥 + 3
   when 𝑥 = -3 when 𝑥 = 1
   𝑦 = -3 + 3 = 0 𝑦 = 1 + 3 = 4
   (-3,0) (1,4)

These can be checked by substituting the values into the other equation.

𝑦 = 𝑥² + 3𝑥
for (-3,0) for (1,4)
0 = (-3)² + 3(-3) 4 = (1)² + 3(1)

Both correct!

Example

Solve the simultaneous equations

𝑦 = 2𝑥 - 3
2 = 𝑥² + 𝑦²

It is not possible to equate the equations since the second equation is not in the form y = __.
Instead one of the letters can be eliminated by substitution.

Example

Solve the simultaneous equations

𝑥𝑦 = 12

𝑦 - 3𝑥 + 9 = 0

In this case neither equation is in the form y = __.

In order to eliminate it is necessary to rearrange one of the equations and then substitute into the other equation.

Solution:

1. Eliminate one of the letters from both equations by substitution
   Rearranging the second equation to get it into the form 𝑦 = __

𝑦 = 3𝑥 - 9

This can be substituted for the y in the first equation.

𝑥𝑦 = 12
𝑥(3𝑥 - 9) = 12

2. Calculate the values of the remaining letter 𝑥𝑦

𝑥(3𝑥 - 9) = 12
3𝑥² - 9𝑥 - 12 = 0 - divide all terms by 3
𝑥² - 3𝑥 - 4 = 0
(𝑥 - 4)(𝑥 + 1) = 0

𝑥 = 4 𝑥 = -1

3. Substitute these back into one of the equations to find the values of the other letter

𝑥𝑦 = 12
When 𝑦 = 4 𝑦 = -3
When 𝑦 = -1 𝑦 = -12

(4,3) (-1,-12)

These can be checked by substituting the values into the other equation.

𝑦 = 3𝑥 - 9
(4,3) (-1,-12)
3 = 3(4) - 9 -12 = 3(-1) -9

Both correct!