Challenge 1 - Broken squares
Challenge 1 is all about making squares and breaking squares.
Maths teacher Chris Smith and pupils from Grange Academy are here to explain.
The Maths Week Scotland Daily Challenges have been set by the Scottish Mathematical Council.
Mr Smith: This problem is all about squares.
Using a construction kit, with 12 straight rods and 9 connectors in the corners, we can make this design:
It has 4 small squares (unit squares) and 1 outer square which has side 2, and so it contains 5 squares altogether.
We could break all the squares by removing just 3 rods. Here’s one way that could be done:
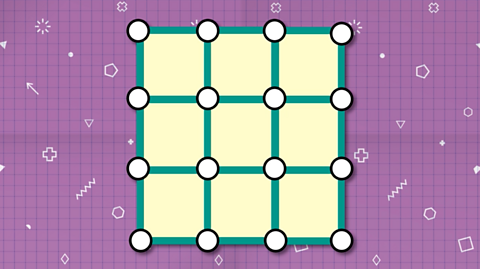
Now here’s a larger design with a greater number of squares:
How many squares of all sizes does it contain?
AND, What is the smallest number of rods that need to be removed so that all the possible squares are broken?
Explain your answer.
Pupil: Think about how many different sizes of squares you can find.
Pupil: Bear in mind that squares can overlap each other.
Pupil: You only need to remove one rod to break apart any size of square.
Pupil: Try your best.
So here's the challenge:
This problem is all about squares.
A large model has been made from a construction kit with rods and connectors.
How many squares of all sizes does it contain?
And what is the smallest number of rods that need to be removed so that all the possible squares are broken?
Need a hint?
- Think about how many different sizes of squares you can find.
- Bear in mind that squares can overlap each other.
- You only need to remove one rod to break apart any size of square.
Solution
Worked out the answer? Here's how you can do it.
Mr Smith Did you work out how many squares were in our model?
Let's look at how we got our answer.
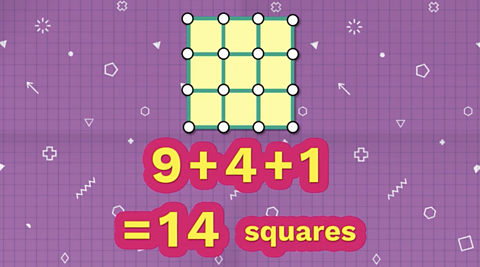
If we start counting the smallest squares, there are nine, plus four medium-sized squares and one large outer square.
So nine plus four plus one gives us 14 squares in all.
And for the second part, what was the smallest number of rods that need to be removed so that all the possible squares are broken?
There are a few ways to go about this: you could break the squares in order of their different sizes, starting with the biggest square side of 3.
Another way would be to pick a corner and work your way around the squares from there.
To break all 14 squares, 6 rods need to be removed.
This solution is just one way of solving this. Have you found any others?
Great job if you made a breakthrough with this challenge.
Part 1
Step 1
If we start counting the smallest squares, there are:
- 9 unit squares
- 4 squares with sides of two
- 1 outer square with sides of three.
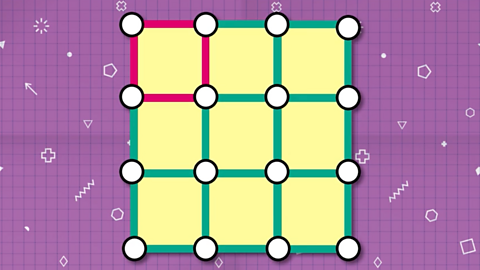
Image caption, There are 9 unit squares (squares with sides one rod long).
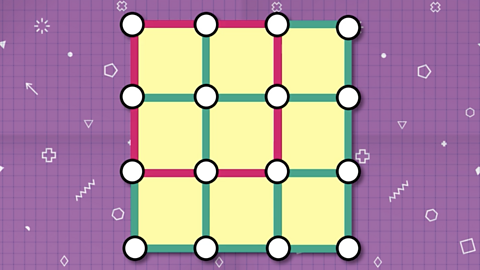
Image caption, There are four squares with sides of two rods.
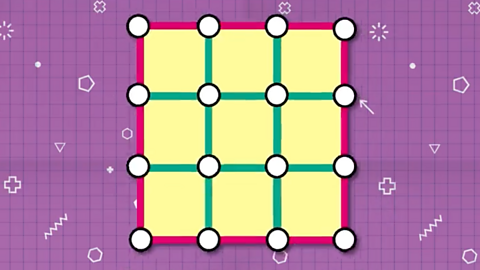
Image caption, There is one large square with sides of three rods.
1 of 3
Step 2
So 9 + 4 + 1 = 14 squares in total within this large model.

Part 2
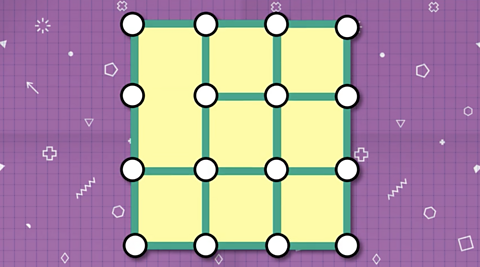
For Part 2, what was the smallest number of rods that need to be removed so that all the possible squares are broken?
There are a few ways to go about this: you could break the squares in order of their different sizes, starting with the biggest square with sides of 3, or starting with the small unit squares.
Another way would be to pick a corner and work your way around the squares from there.
Here's one way to do it.

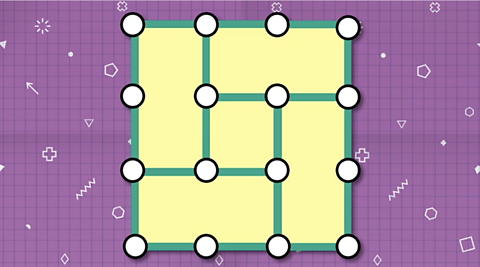
Step 3
Work your way round the unit squares. Remove the rod from the middle of each pair of squares.
That's a total of 4 rods.

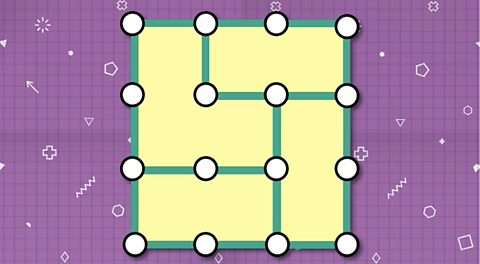
Step 4
This leaves you will the central unit square and the large outer square.
Remove a fifth rod to break the central unit square.

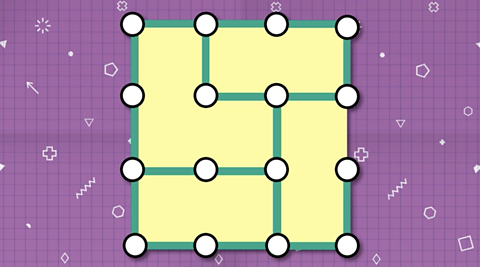
Step 5
Now remove one of the outer rods to break the largest square.
You're done!
So, to break all 14 squares, 6 is the minimum number of rods that needs to be removed.

Maths problem solving. collectionMaths problem solving
Try out Maths Week Scotland challenges from previous years.

Maths Week Scotland. External LinkMaths Week Scotland
Find more maths challenges and activities at the Maths Week Scotland website.

More on Maths Week Scotland 2025
Find out more by working through a topic
